Quantum Computing auf den Punkt gebracht

Quantencomputing is ein neuer Ansatz in der Informatik, der die Grundprinzipien der Quantenmechanik nutzt, um Berechnungen durchzuführen. Berechnungen mit Quantencomputern versprechen dabei einige Probleme effizient lösen zu können. Dies sind zum Beispiel Primfaktorzerlegung, Quantensimulation, Optimierung von Such-Abfragen und das maschinelle Lernen; Quantencomputing hat dabei die Perspektive Berechnungen durchzuführen, die sogar die Fähingkeiten der größten Supercomputer übersteigen.

Die große Leistungsfähigkeit von Quantencomputing beruht im Wesentlichen auf zwei Eigenschaften der Quantenmechanik. Diese sind Superposition und Verschränkung und leiten sich aus der parallelen Wellen- und Teilcheneigenschaft der Materia ab (Welle und Teilchen-Dualismus). Qiskit ist ein Software Development Kit (SDK) für das Quantencomputing, welche diese quantenmechanischen Prinzipien mit Hilfe von programmierbaren Quantenschaltkreisen umsetzt. Durch Quantengatter, Programmieranweisungen und klassischer Steuerlogik, erlauben es Quantenschaltungen, komplexe Algorithmen und Anwendungen auf abstrakte Weise darzustellen und auf einem Quantencomputer auszuführen. Im Kern ist Qiskit ein Programmier-Instrument, um Quantenschaltkreise zu erstellen, zu optimieren und auszuführen. Sehr häufig arbeiten diese Quantenschaltkreise eng mit klassischen Rechenresourcen zusammen, um somit zum Beispiel numerische Optimierungen in der Chemie, der Physik, dem maschinellen Lernen oder der Finanzindustrie durzuführen. Im folgenden wird ein kurzer Überblick über die wesentlichen Eigenschaften des Quantencomputing gegeben, und anhand von Qiskit mit praktischen Beispielen erläutert. Interessierte Leser mögen dabei auf zusätzliche vertiefendere Fachliteratur zurückgreifen.

Interferenz

Ein Quantencomputer arbeitet analog zu einem klassischen Computer auf der Basis von Bits. Beim klassischen Computer können diese Bits nur zwei Zustände einnehmen, nämlich den Zustand 0 oder den Zustand 1. Ein Quantenbit oder qubit kann allerdinds zusätzlich zur 0 und 1 noch eine Linearkombination dieser beiden Zustände darstellen. Diese Linearkombination wird Superposition oder Superposition von Zuständen genannt.

Um den Nutzen der quantenmechanischen Superposition besser zu verstehen, wird zuerst ein klassisches Analogon betrachtet: Rauschunterdrückung. Diese Technik wird zum Beispiel in Kopfhörern dazu benutzt, ungewollte Geräusche zu unterdrücken indem man Superposition zusammen mit Interferenz nutzt. Dabei wird ein Ton mit etwa gleicher Amplitude und Frequenz wie der Ungewollte erzeugt, allerding mit einer Phasenverschiebung von \(\pi\) (oder jedem ungeraden ganzzahligen Vielfachen von \(\pi\)).

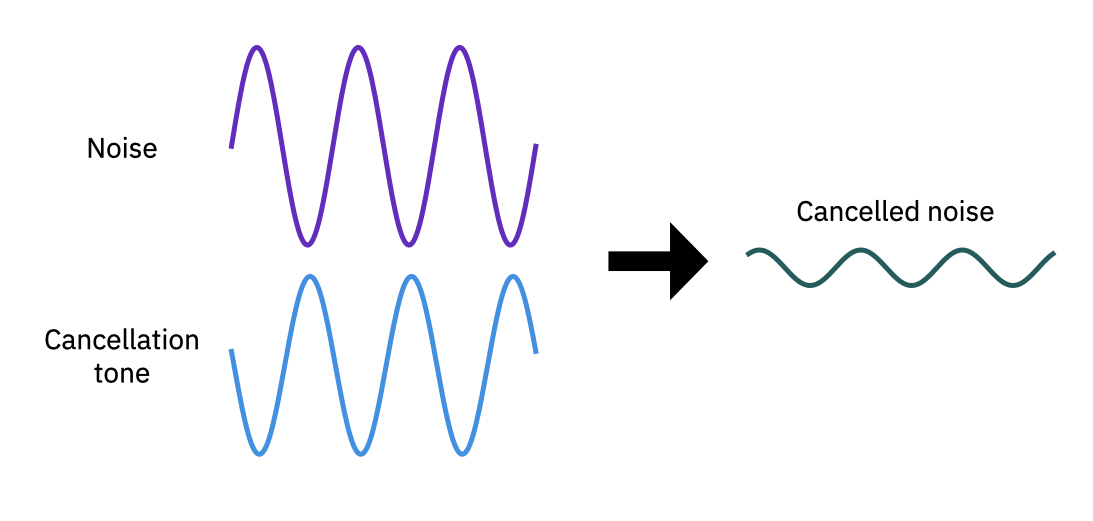
Abb. 1 Ungefähre Rauschunterdrückung durch einen Ton von nahezu gleicher Amplitude und einer Phasenverschiebung von :math:` sim pi `.

Wie oben gezeigt, führt eine Phasendifferenz die ungefähr einem ungeraden Vielfachen von :math:` pi ` entspricht, bei Überlagerung der beiden Wellen zu Interferenzen und einer im Vergleich zum Original deutlich reduzierten Leistung. Das Ergebnis ist ein erheblich verrauschten Signal. Obwohl die Verarbeitung durch digitale Schaltkreise erfolgt, sind Amplitude und Phase kontinuierliche Variablen, die nie perfekt aufeinander abgestimmt werden können, was zu einer unvollständigen Korrektur führt.

Eine allgemeine Berechnung auf einem Quantencomputer erfolgt in sehr ähnlicher Weise wie die Rauschunterdrückung. Zunächst werden alle möglichen Berechnungszustände in Superposition gebracht. Diese wird dann als Eingabe für eine :ref:` Quantenschaltung <qc-intro-circuits>` verwendet, die die Komponenten der Superposition nach einem vorgegebenen Algorithmus selektiv zur Interferenz bringt. Was nach der Aufhebung der relativen Amplituden und Phasen des Eingangszustandes bleibt, ist die Lösung der von der Quantenschaltung durchgeführten Berechnung.

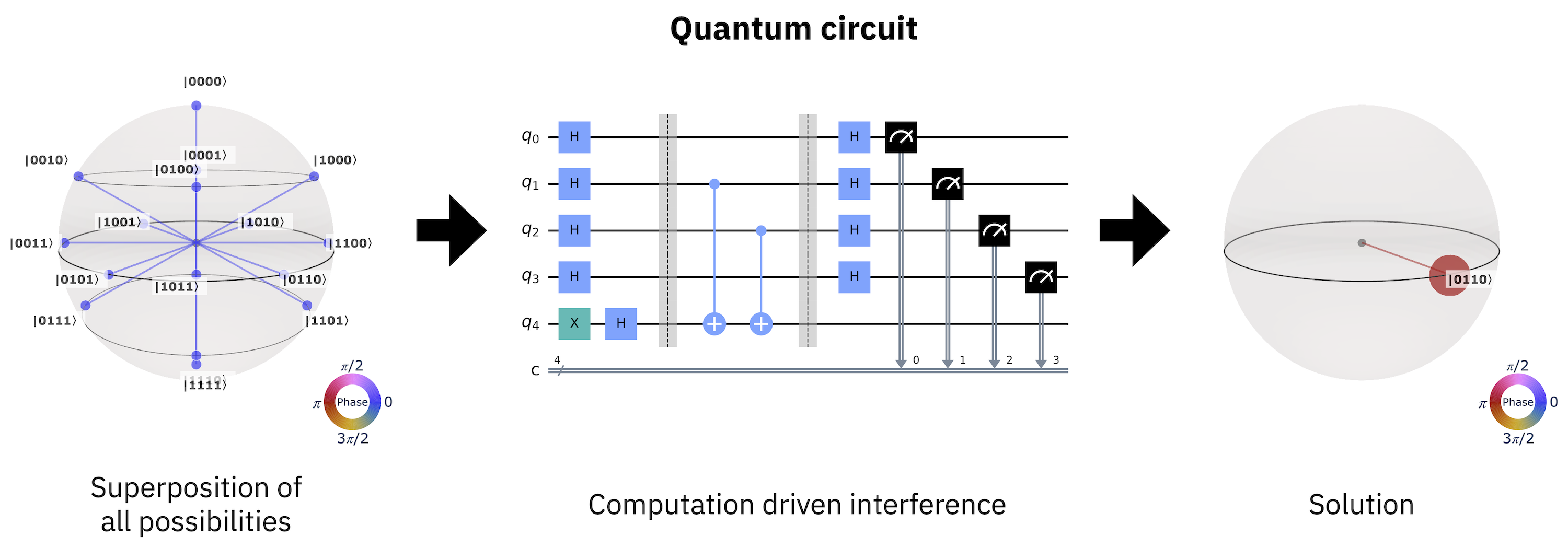
Abb. 2 Quantenberechnung als ein Porzess zur Erstellung von Interferenzen.

Verschränkung

Das zweite Prinzip der Quantenmechanik, das die Quantenberechnung benutzen kann, ist das Phänomen der ** Verschränkung **. Die Verschränkung bezieht sich auf Zustände von mehr als einem Qubit (oder Teilchen im Allgemeinen), in denen der kombinierte Zustand der Qubits mehr Informationen enthält, als die Qubits unabhängig voneinander. Die überwältigende Mehrheit der Multi-Qubit-Quanten-Zustände sind verschränkt und stellen eine wertvolle Ressource dar. So können beispielsweise verschränkte Zustände zwischen Qubits für die Quanten-Teleportation verwendet werden, bei denen ein geteilter verschränkter Zustand von zwei Qubits unabhängig von der relativen physikalischen Nähe der Qubits zur Übertragung von Informationen von einem Qubit auf einen anderen manipuliert werden kann. Verschränkte Zustände, wie natürliche Zustände von Quantensystemen, sind auch in Disziplinen wie Quantenchemie und Quantensimulation von Bedeutung, bei denen die Lösung (en) oft die Form von verschränkten Multiqubit-Zuständen annehmen. Man kann auch hochverschränkte Quantenzustände von mehreren Qubits nutzen, um beispielsweise zertifizierbare Zufallszahlen zu erzeugen. Es gibt sogar ein ` Qiskit-Paket <https://qiskit-rng.readthedocs.io/en/latest/>` _ um dies zu tun!

Quantenschaltungen

Algorithmen und Anwendungen, die quantenmechanische Ressourcen nutzen, können einfach und effizient in der Sprache von ** Quantenschaltkreisen * * geschrieben werden. Ein Quantenschaltkreis ist eine Rechenroutine, die aus kohärenten Quantenoperationen auf Quantendaten besteht, wie sie in Qubits gehalten werden, und parallel dazu ablaufenden klassischen Echtzeit-Berechnungen. Jede horizontale Linie oder Draht in einer Schaltung stellt ein Qubit dar, wobei das linke Ende des Drahtes die ursprünglichen Quantendaten darstellt und das Rechte die endgültigen Quantendaten, die durch die Berechnung des Quantenschaltkreises erzeugt werden. Operationen auf Qubits werden durch Boxen dargestellt, die auf diesen Drähten platziert werden.

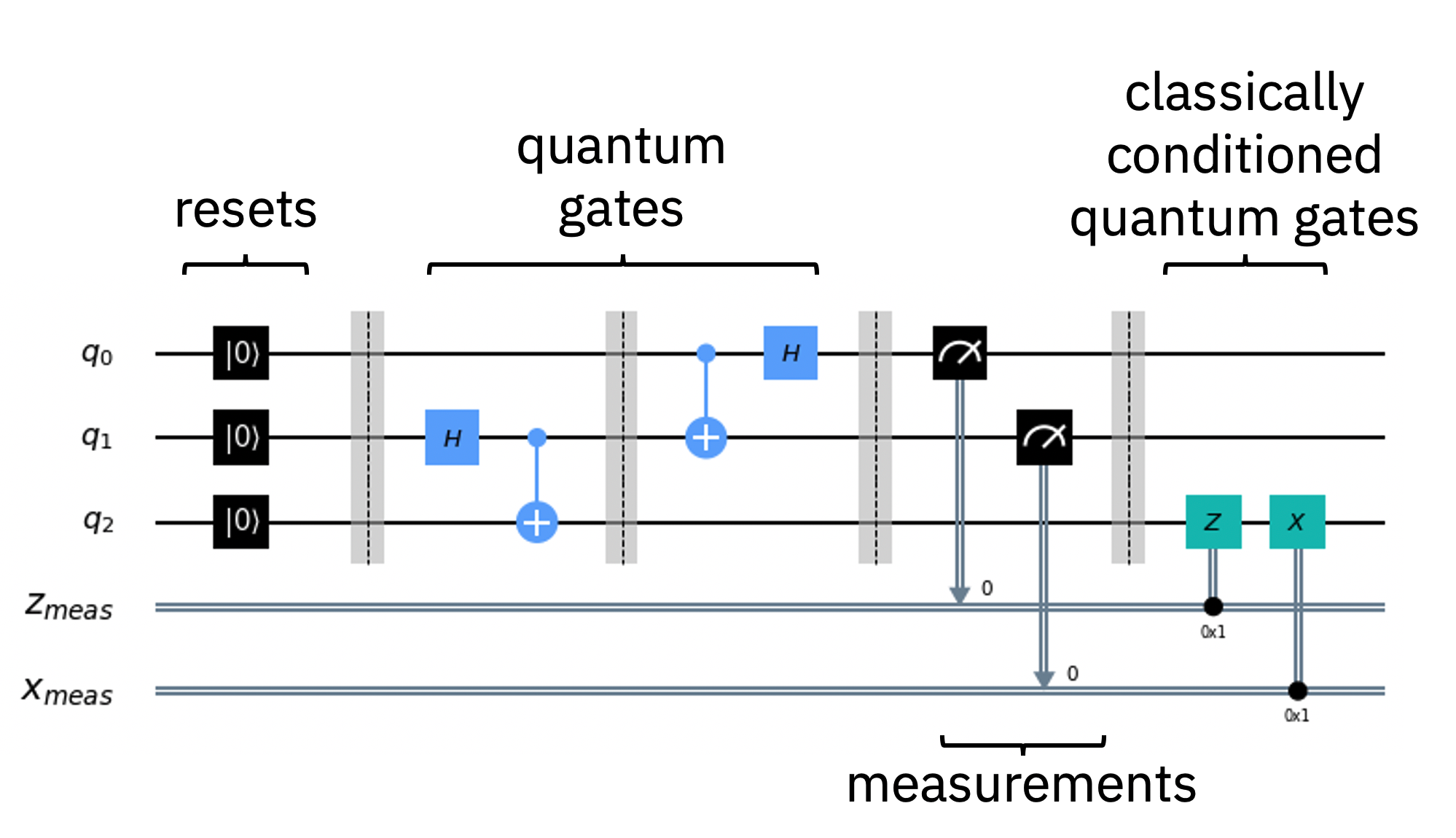
Abb. 3 Tiefere Einblicke in die Teleportation von Quantenzuständen.

Quantenschaltkreise ermöglichen es einem Quantencomputer, klassische Informationen zu übernehmen und eine klassische Lösung herauszugeben, indem Quantenprinzipien wie :ref:` Superposition <qc-intro-superposition>` und :ref:` Verschränkung <qc-intro-entanglement>` für die Berechnung genutzt werden.

Ein typischer Quanten-Algorithmus-Workflow besteht aus:

• Das Problem, das wir lösen wollen,

• Ein klassischer Algorithmus, der eine Beschreibung eines Quantenschaltkreises erzeugt,

• Der Quantenschaltkreis, der auf Quantenhardware betrieben werden muss,

• Und die klassische Output-Lösung für das Problem, das es erzeugt.

Quanten-Gates sind die Grundfunktionen für Quantendaten. Diese „unitären“ Transformationen sind das Kernstück eines Quantenschaltkreises. Die Vorgänge sind Informationserhaltend und umkehrbar. Manche Gatter wie \(X\) (auch geschrieben als \(\oplus\)) und \(CX\) haben klassische Analogien wie Bit-flip und \(XOR\) Operationen, andere nicht. Das Hadamard (\(H\)) Gatter, zusammen mit den parametrisierten Rotationen \(rX(\theta)\) und \(rY(\theta)\), generiert Superposition-Zustände, während Gates wie \(Z\), \(rZ(\theta)\), \(S\), und \(T\) Phasen erzeugen, die für Interferenzen verwendet werden können. Zwei-Qubit-Gates wie das \(CX\) Gatter werden verwendet, um Verschränkung zwischen Qubit-Paaren zu erzeugen, oder die Phase von einem Qubit zum anderen zu „kicken“. Im Gegensatz zu Gates, gehen bei Operationen wie einer „Messung“ (repräsentiert durch das Zählersymbol mit einer Linie zum Zielregister) teilweise Informationen über den Zustand eines Qubits, wie z.B. die Phase verloren, um diese Information als klassischen Bit darstellen zu können. Es ist zu beachten, dass nur mit \(H\), \(rZ(\theta)\), \(CX\) Messgattern, also Universellen Gate-Gruppen Quantenschaltkreise aufgebaut werden können. Einschließlich derer, die die Dynamik jedes physikalischen Systems in der Natur effizient berechnen.

Einige Workloads enthalten eine erweiterte Folge von verschachtelten Quantenschaltkreisen und klassischen Berechnungen, wie zum Beispiel Variations-Quantenalgorithmen, die Quantenschaltkreise innerhalb einer Optimierungsschleife ausführen. Für diese Workloads erhöht sich die Systemleistung erheblich, wenn die Quantenschaltkreise parametrisiert werden und Übergänge zwischen der Schaltkreissausführung und der nicht aktuellen klassischen Berechnung effizient gemacht werden. Folglich definieren wir ** Nahzeitberechnung **, um auf Berechnungen mit Algorithmen zu verweisen, die von mehrfacher Verwendung bestimmter Quantenschaltkreise Gebrauch macht auf Hardware, die entwickelt wurde, um die Rechenzeit zu verkürzen. In der Nahzeitberechnung erfolgt die klassische Berechnung auf einer zeitlichen Skala, die länger ist als die Kohärenz der Quantenberechnung. Im Gegensatz dazu erfolgt bei der ** Echtzeitberechnung ** die klassische Berechnung innerhalb der Dekohärenzzeit der Quantenvorrichtung.

Die Konstruktion komplexer Quantenschaltungen mit minimalem Aufwand ist das Herzstück von Qiskit, das eine Vielzahl von Funktionen unterstützt und Ihre Schaltungen an eine Reihe von Quantencomputern oder klassischen Simulatoren senden kann. Mit nur wenigen Zeilen Code ist es möglich, komplexe Schaltungen wie die obige zu konstruieren.

qr = QuantumRegister(3, 'q')
cr = ClassicalRegister(2, 'zx_meas')
qc = QuantumCircuit(qr,cr)
qc.reset(range(3))
qc.barrier()
qc.h(1)
qc.cx([1,0],[2,1])
qc.h(0)
qc.barrier()
qc.measure([0,1], [0,1])
qc.barrier()
qc.z(2).c_if(cr, 1)
qc.x(2).c_if(cr, 2)

Quantencomputer

Abb. 4 Ein Blick in das Innere des IBM Quantum System One.

Quantencomputer, die mittels Quantenschaltkreisen programmiert werden, können im Prinzip aus jeder Quantentechnologie konstruiert werden, wenn diese Single- und Multi-Qubit-Gatte Operationen mit hoher Zuvarlässigkeit realisieren kann. Derzeit werden aktiv Architekturen entwickelt, die auf superleitenden Schaltkreisen, Ionenfallen, Halbleiterquantenpunkten, Photonen und neutralen Atomen basieren. Viele sind über das Internet für Nutzer zugänglich. Qiskit kapselt die Architektur des jeweiligen Quantensystems und kompiliert der Quantengattertopologie eines Gerätes entsprechende Quantenschaltungen, bildet die Schaltkreisbefehle auf dessen nativen Satz von Gates ab und optimiert die resultierende Quantenschaltung für eine erhöhte Genauigkeit.

Wie bei dem Beispiel für Rauschunterdrückung oben sind die Amplitude und Phase von Qubits kontinuierliche Freiheitsgrade, auf denen Operationen niemals exakt durchgeführt werden können. Diese Gate-Fehler, zusammen mit Rauschen aus der Umgebung eines Quantencomputers, können zusammen genommen eine Berechnung zerstören, wenn das nicht beim Kompilierungsprozesses mit berücksichtigt wird und entsprechende Korrekturen durchgeführt werden, um eine hohe Zuverlässigkeit auf störanfälligen derzeitigen Quantensystemen zu erhalten, wie sie heute üblich sind. Qiskit ist in der Lage, eine breite Palette von Gerätekalibrierungsmetriken (siehe Abbildung unten) in seiner Kompilierungsstrategie zu berücksichtigen, und kann eine optimale Gruppe von Qubits auswählen, auf denen eine bestimmte Quantenschaltung ausgeführt werden soll. Darüber hinaus bietet Qiskit eine Sammlung von rauschunterdrückenden Techniken für die Extraktion einer originalgetreuen Darstellung der Ausgabe von Quantenschaltungen an.

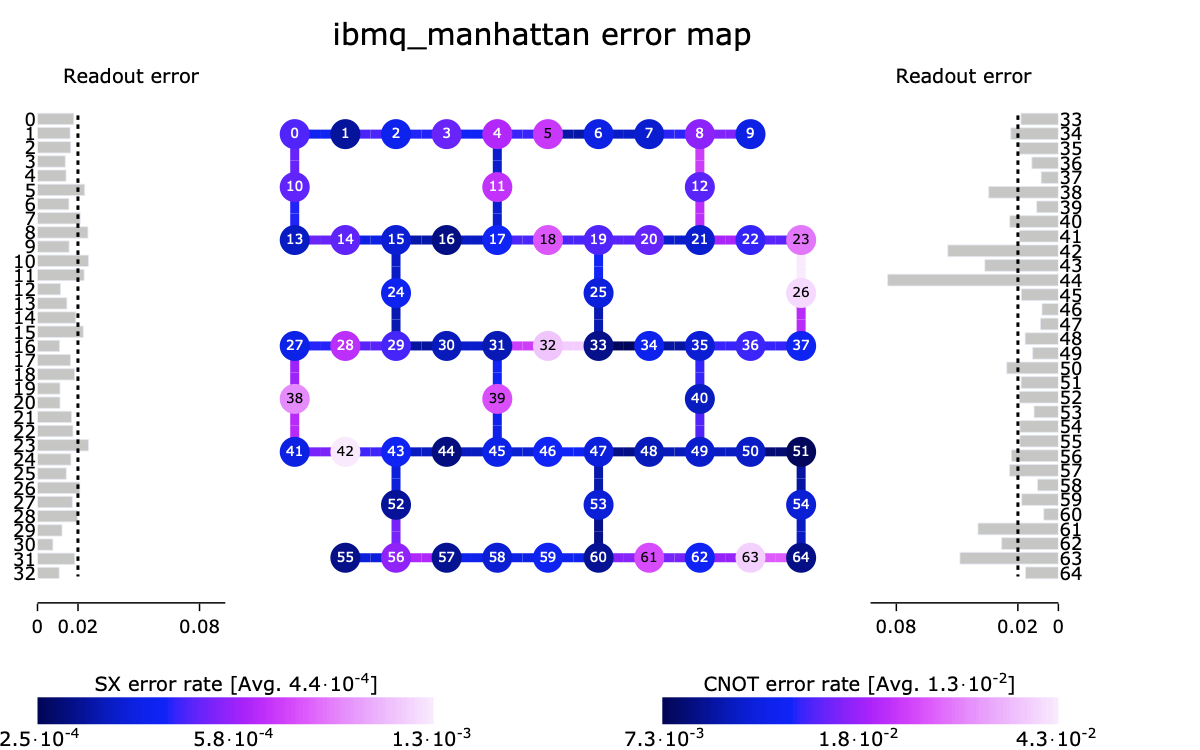
Abb. 5 Topologie und Fehlerraten für das IBM Quantum ibmq_manhattan System.

Weitere Informationen

Hoffentlich haben wir bei dem Leser einen Eindruck über die Leistungsfähingkeit von Quantencomputern verschaffen können und Interese auf weiterführenden Lernstoff geweckt. Wenn ja, gibt es mehrere Ressourcen, die sehr hier hilfreich sein könnten:

• ` Erste Schritte mit Qiskit <getting_started.html>` _- Direkt mit Qiskit loslegen.

• “ Leitfaden Quantencomputing <https://quantum-computing.ibm.com/docs/iqx/guide/>` _: Eine anfängerfreundliche, physik-basierte Einführung, die von einigen Gründern des Quantencomputings geschrieben wurde und den interaktiven Circuit-Composer nutzt.

• Qiskit textbook : A university quantum algorithms/computation course supplement based on Qiskit.