L’informatique quantique en bref

L’informatique quantique représente un nouveau paradigme dans le calcul qui utilise les principes fondamentaux de la mécanique quantique pour effectuer les calculs. Si vous lisez ceci, vous avez sans aucun doute entendu que la promesse du calcul quantique réside dans la possibilité de réaliser efficacement un certain nombre de de tâches telles que la factorisation en nombres premiers , la simulation quantique et certains problème d’optimisation; des calculs qui dont la taille dépasse les capacités des plus grands d’ordinateurs classiques.

La puissance de l’informatique quantique repose sur deux des pierres angulaires de la mécanique quantique, à savoir la superposition d’états et l’intrication qui mettent en évidence certains aspects de la dualité onde-particule. Qiskit est un environnement de développement (SDK) permettant de réaliser des calculs quantiques en utilisant ces principes de mécanique quantique avec le langage des circuits quantiques. Ces circuits sont constitués de portes quantiques, d’instructions et de logique de contrôle classique, et ils permettent d’exprimer des algorithmes et des applications complexes pour être exécutés sur un ordinateur quantique. A la base, Qiskit est un moteur quantique de construction, d’optimisation et d’exécution des circuits quantiques. Les algorithmes et les applications qui sont construites par dessus tirent parti des circuits quantiques, souvent de concert avec les ressources informatiques classiques, pour résoudre des problèmes d’optimisation, de chimie quantique, de physique, d’apprentissage automatique et de finance. Dans ce qui suit, nous donnons un bref aperçu de l’informatique quantique et de la façon dont Qiskit est utilisé à chaque étape. Les lecteurs intéressés seront orientés vers des documents plus détaillés afin d’obtenir de plus amples renseignements.

Interférence

Comme un ordinateur classique, un ordinateur quantique fonctionne avec des bits. Cependant, alors que les bits classiques ne peuvent être trouvés que dans les états 0 et 1, un bit quantique, ou un qubit, peut représenter les valeurs 0 et 1, ou des combinaisons linéaires de ces deux valeurs. Ces combinaisons linéaires sont connues sous le nom de superpositions (ou états de superposition) et permettent de représenter et de traiter de façon exponentielle de nombreux états logiques simultanément.

Pour voir comment cette ressource est utilisée dans le calcul quantique, nous nous tournons d’abord vers un analogue classique : l’annulation du bruit. L’annulation du bruit, comme on le trouve dans les écouteurs annulant le bruit ambiant par exemple, est réalisée en employant le principe de superposition et le princidpe d’interférence pour réduire l’amplitude du bruit non désiré en générant un ton de même fréquence et amplitude, mais déphasé d’une valeur de \(\pi\) (ou tout autre multiple entier impair de \(\pi\)).

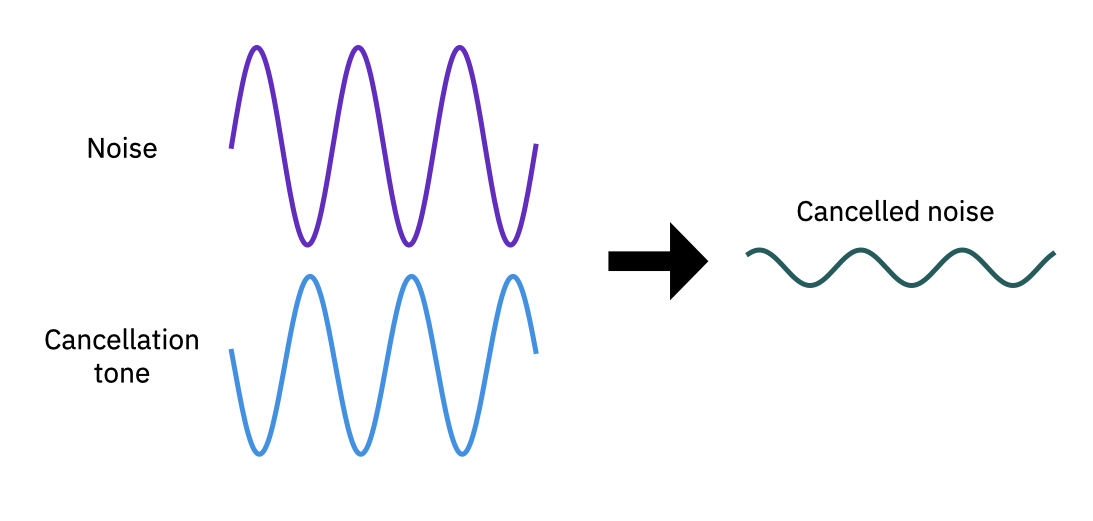
Fig. 1 Annulation approximative d’un signal parasite par un signal d’amplitude presque égale et décalé par une phase de \(\sim \pi\).

Comme indiqué ci-dessus, lorsque la différence de phase est proche d’un multiple impair de \(\pi\), la superposition des deux ondes entraîne une interférence, et une sortie qui est significativement réduite par rapport à l’original. Le résultat correspond au signal recherché non encombré par le bruit. Bien que ce traitement soit effectué par des circuits numériques, l’amplitude et la phase sont des variables continues qui ne peuvent jamais être réglées parfaitement, ce qui entraîne une correction incomplète.

Un calcul général sur un ordinateur quantique procède de la même manière que l’annulation du bruit. Pour commencer, on prépare une superposition de tous les états de calcul possibles. Ceci est ensuite utilisé comme entrée dans un circuit quantique qui interfère sélectivement les composantes de la superposition selon un algorithme donné. Ce qui reste après l’annulation des amplitudes et des phases relatives de l’état d’entrée est le résultat du calcul effectué par le circuit quantique.

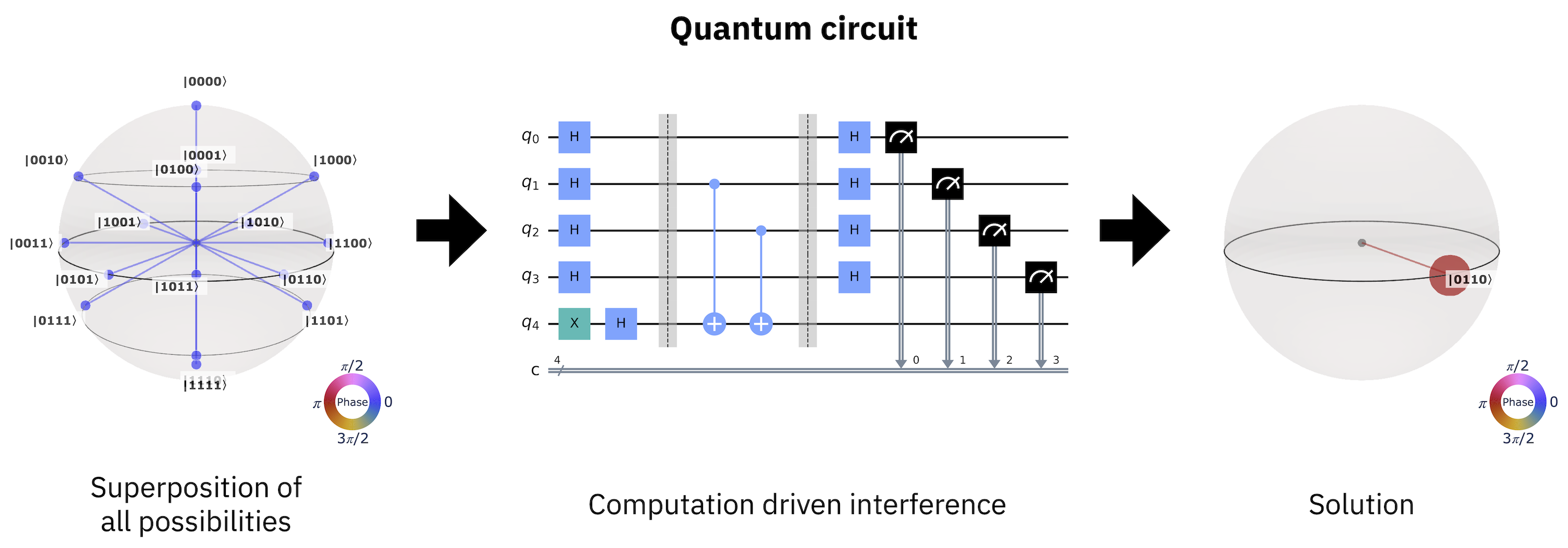
Fig. 2 Le calcul quantique en tant que processus de génération d’interférence.

Intrication

Le deuxième principe de la mécanique quantique que le calcul quantique peut utiliser est le phénomène d”intrication. L’intrication fait référence à des états composé de plus d’un qubit (ou particules en général) dans lesquels l’état combiné des qubits contient plus d’information que les qubits ne le peuvent indépendamment les uns des autres. La très grande majorité des états quantiques multiqubits sont intriqués et représentent une ressource précieuse. Par exemple, les états intriqués entre les qubits peuvent être utilisés pour la téléportation quantique, où un état intriqué partagé de deux qubits peut être manipulé pour transférer des informations d’un qubit à un autre, quelle que soit la proximité physique relative des qubits. Les états intriqués, en tant qu’états naturels des systèmes quantiques, sont également importants dans des disciplines telles que la chimie quantique et la simulation quantique où les solutions prennent souvent la forme d’états multiqubit intriqués. On peut aussi utiliser des états quantiques très intriqués de plusieurs qubits pour, par exemple, générer des nombres aléatoires certifiés. Il y a même un module Qiskit pour faire cela !

Circuits quantiques

Les algorithmes et les applications qui utilisent les principes de la mécanique quantique peuvent être écrits facilement et efficacement dans la langue des circuits quantiques. Un circuit quantique est une routine de calcul consistant en des opérations quantiques cohérentes sur des données quantiques, telles que celles qui sont stockées dans des qubits, et des calculs classiques en parallèle et en temps réel. Chaque ligne horizontale, ou fil, dans un circuit représente un qubit, avec l’extrémité gauche du fil étant les données quantiques initiales, et la droite étant les données quantiques finales générées par le calcul du circuit quantique. Les opérations sur les qubits peuvent être placées sur ces fils et sont représentées par des boîtes.

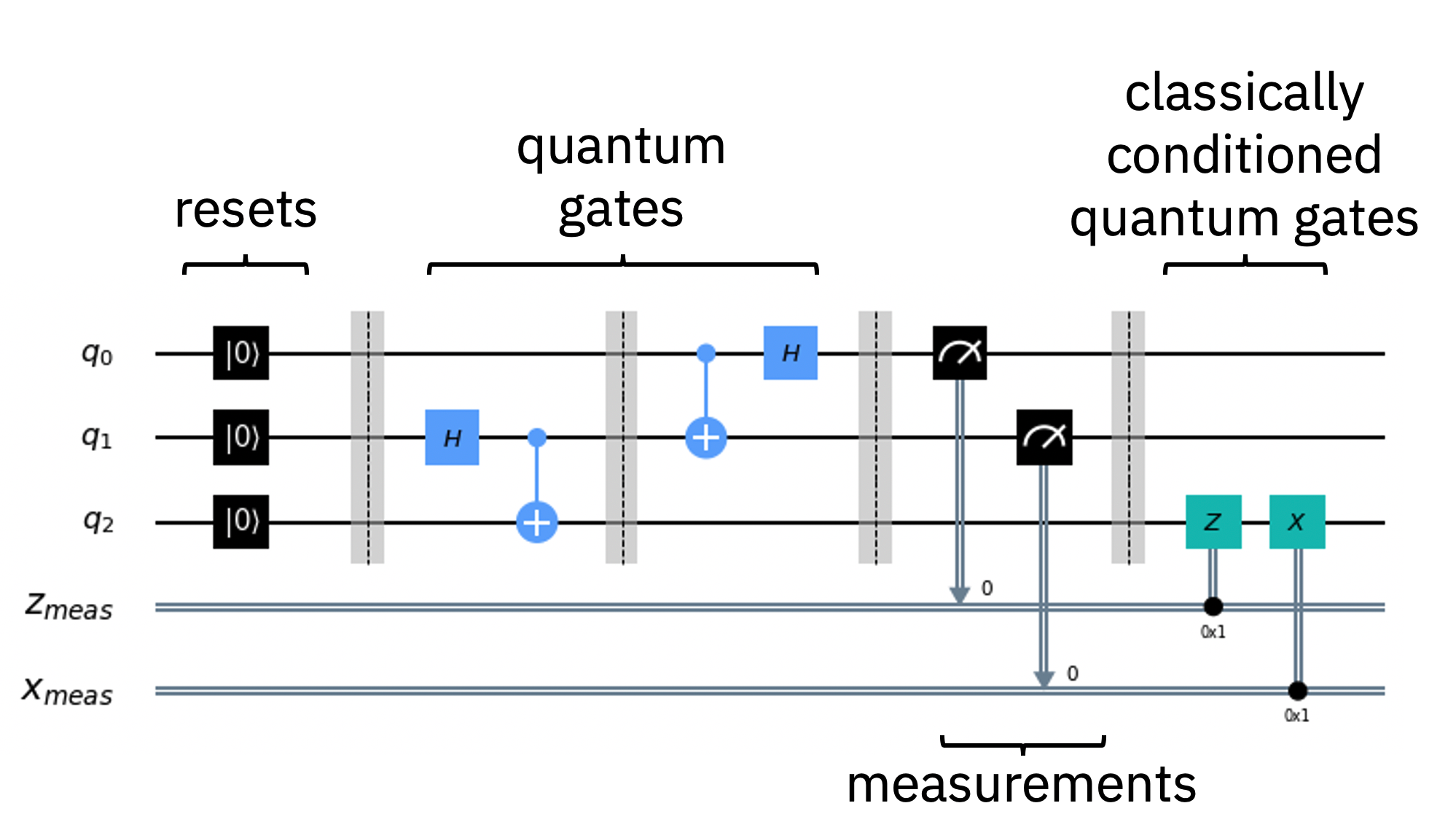
Fig. 3 Circuit de téléportation d’état quantique revisité.

Les circuits quantiques permettent à un ordinateur quantique d’utiliser des informations classiques et de produire une solution classique, en utilisant des principes quantiques tels que interférence et intrication pour effectuer le calcul.

Un algorithme quantique typique consiste en:

• Le problème que nous voulons résoudre,

• Un algorithme classique qui génère une description d’un circuit quantique,

• Le circuit quantique qui doit être exécuté sur du matériel quantique,

• Et la solution au problème sous forme de sortie classique.

Les portes quantiques executent les opérations primitives sur les données quantiques. Les portes quantiques représentent des transformations réversibles préservant les informations réversibles sur les données quantiques stockées dans les qubits. Ces transformations « unitaires » représentent les commposants élémentaires quantiques d’un circuit quantique. Certaines portes telles que \(X\) (également écrite comme \(\oplus\)) et \(CX\) ont des analogues classiques tels que les opérations bit-flip et \(XOR\) respectivement, mais ce n’est pas le cas pour toutes les portes. La porte de Hadamard (\(H\)), ainsi que les rotations paramétrées \(rX(\theta)\) et \(rY(\theta)\), génerent des états de superposition, tandis que les portes telles que \(Z\), \(rZ(\theta)\), \(S\), et \(T\) appliquent des phases qui peuvent être utilisées pour des interférences. Les portes à deux qubits comme la porte \(CX\) sont utilisées pour générer une intrication entre les qubits, ou pour « expulser » la phase d’un qubit à l’autre. Contrairement aux portes, l’opération de « mesure », représentée par le symbole d’un compteur dans une boîte avec une ligne se connectant à un fil « cible », permet d’extraire des informations partielles sur l’état d’un qubit, souvent en perdant la phase, pour être capable de le représenter comme un bit classique et d’écrire ce bit classique sur le fil cible (souvent un fil entièrement classique dans un dispositif de lecture). C’est la façon typique de prendre des informations des données quantiques dans un appareil classique. Notez qu’en utilisant uniquement les portes \(H\), \(rZ(\theta)\), \(CX\), et des portes de mesure (constituant un ensemble de portes universelles), nous pouvons construire n’importe quel circuit quantique, y compris ceux qui calculent efficacement la dynamique de n’importe quel système physique dans la nature.

Certaines charges de travail contiennent une séquence étendue de circuits quantiques entrelacés de calculs classiques, par exemple des algorithmes quantiques variationnels exécutent des circuits quantiques dans une boucle d’optimisation. Pour ces charges de travail, la performance du système augmente considérablement si les circuits quantiques sont paramétrés, et les transitions entre l’exécution du circuit et le calcul classique non courant sont rendues efficaces. Par conséquent, nous définissons le calcul proche du temps réel pour faire référence à des calculs avec des algorithmes qui font une utilisation répétée de circuits quantiques avec du matériel développé pour accélérer le temps de calcul. En temps quasi-réel, le calcul classique se produit sur une échelle plus longue que le temps de cohérence des qubits. Contrairement au calcul en temps réel, où le calcul classique se produit plus rapidement que le temps de décohérence de l’appareil quantique.

La construction de circuits quantiques complexes avec un effort minimal est au cœur de Qiskit, qui prend en charge un grand ensemble d’opérations, et peut être transmis à une gamme d” ordinateurs quantiques ou à des émulateurs classiques. Avec seulement quelques lignes de code, il est possible de construire des circuits complexes comme celui ci-dessus.

qr = QuantumRegister(3, 'q')
cr = ClassicalRegister(2, 'zx_meas')
qc = QuantumCircuit(qr,cr)
qc.reset(range(3))
qc.barrier()
qc.h(1)
qc.cx([1,0],[2,1])
qc.h(0)
qc.barrier()
qc.measure([0,1], [0,1])
qc.barrier()
qc.z(2).c_if(cr, 1)
qc.x(2).c_if(cr, 2)

Ordinateurs quantiques

Fig. 4 Une vue à l’intérieur du système IBM Quantum One.

Les ordinateurs quantiques programmés à l’aide de circuits quantiques sont appelés calculateurs quantiques à portes. De tels systèmes peuvent être construits à partir de n’importe quelle technologie quantique qui permet de définir des éléments de qubits, et de mettre en œuvre des opérations de portes simples et multiqubits avec une haute fidélité. À l’heure actuelle, les architectures basées sur les circuits supraconducteurs, les ions piégés, les quantum-dots à semi-conducteurs, les photons et les atomes neutres sont activement développées, et beaucoup sont accessibles aux utilisateurs sur Internet. Qiskit est agnostique par rapport à l’architecture sous-jacente d’un système quantique donné, et peut compiler un circuit quantique pour correspondre à la topologie d’un appareil quantique, mapper les instructions du circuit sur l’ensemble des porte native de l’appareil, et optimiser le circuit quantique qui en résulte pour une fidélité accrue.

Comme dans le cas de l’exemple d’annulation du bruit ci-dessus, l’amplitude et la phase des qubits sont des degrés de liberté continus sur lesquels les opérations ne peuvent jamais être effectuées exactement. Ces erreurs de portes, ainsi que le bruit de l’environnement dans lequel réside un ordinateur quantique, peuvent conspirer à ruiner un calcul s’ils ne sont pas pris en compte dans le processus de compilation, et peuvent nécessiter des procédures d’atténuation supplémentaires afin d’obtenir une sortie de haute fidélité sur les systèmes quantiques actuels sensibles au bruit. Qiskit est capable de prendre en compte une large gamme de mesures d’étalonnage des dispositifs (voir figure ci-dessous) dans sa stratégie de compilation, et peut sélectionner un ensemble optimal de qubits sur lequel exécuter un circuit quantique donné. De plus, Qiskit héberge une collection de techniques d’atténuation du bruit pour l’extraction d’une représentation fidèle d’une sortie de circuits quantiques.

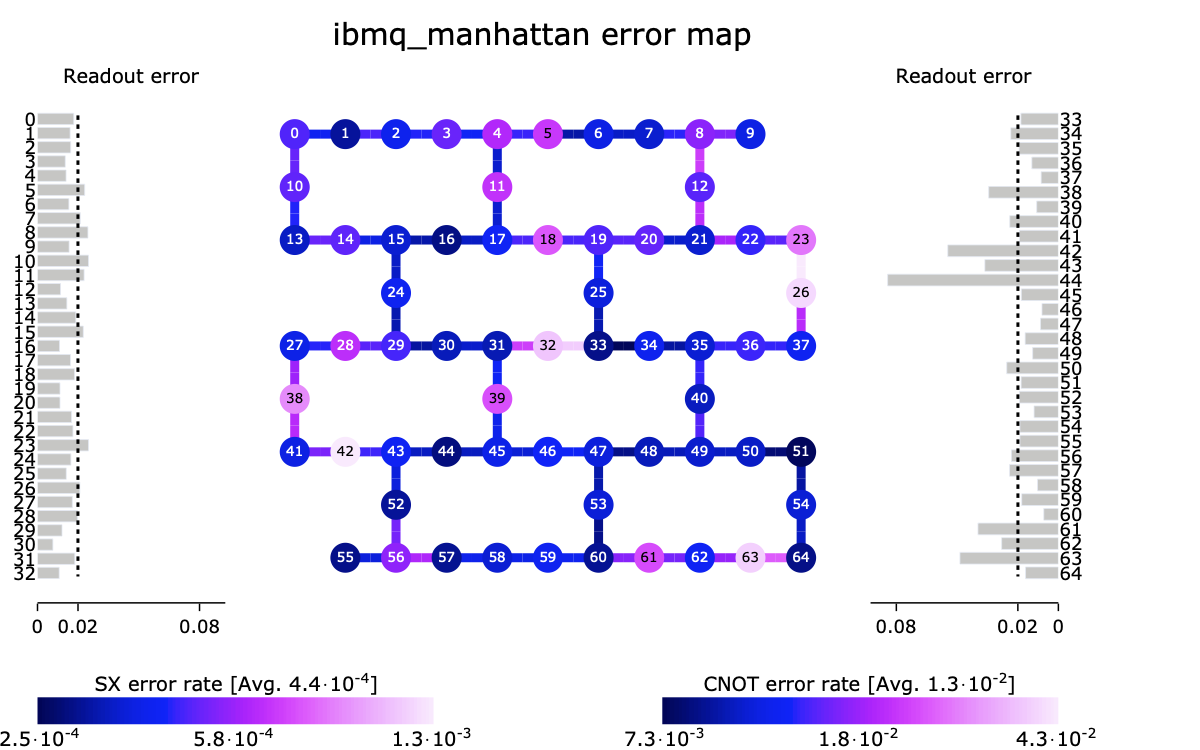
Fig. 5 Topologie et taux d’erreur pour le système IBM Quantum ibmq_manhattan.

A présent où aller ?

Nous espérons avoir donné au lecteur un aperçu de ce que le calcul quantique a à offrir et l’envie d’aller plus loin. Dans ce cas, il y a plusieurs ressources qui peuvent vous intéresser :

• Getting started with Qiskit - Démarrer avec Qiskit.

• Field guide to quantum computing: une introduction progressive et basée sur la physique quantique écrite par certains des fondateurs du calcul quantique et qui utilise le composeur interactif de circuits quantiques.

• Qiskit textbook : A university quantum algorithms/computation course supplement based on Qiskit.