குவாண்டம் கணினிகள் பற்றிய சுருக்கம்#
குவாண்டம் கம்ப்யூட்டிங் கணக்கீட்டில் ஒரு புதிய முன்னுதாரணத்தைக் குறிக்கிறது. இது கணக்கீடுகளைச் செய்ய குவாண்டம் இயக்கவியலின் அடிப்படைக் கொள்கைகளைப் பயன்படுத்துகிறது. நீங்கள் இதைப் படிக்கிறீர்கள் என்றால், குவாண்டம் கணக்கீட்டின் வாக்குறுதி பிரதான காரணிமயமாக்கல், குவாண்டம் உருவகப்படுத்துதல், தேடல், தேர்வுமுறை மற்றும் இயந்திர கற்றல் போன்ற இயற்கணித திட்டங்கள் போன்ற ஒரு சில பணிகளை திறம்படச் செய்வதற்கான சாத்தியத்தில் உள்ளீர்கள் என்பதில் சந்தேகமில்லை. இது பெரிய அளவிலான கிளாசிக்கல் கணினிகளின் திறன்களுக்கு அப்பாற்பட்ட கணக்கீடுகள்.
குவாண்டம் கம்ப்யூட்டிங்கின் சக்தி குவாண்டம் இயக்கவியலின் இரண்டு மூலையில் உள்ளது, அதாவது குறுக்கீடு மற்றும் அலைகளை முன்னிலைப்படுத்தும் முறையே குவாண்டம் கணக்கீட்டின் அம்சங்கள்.Qiskit என்பது குவாண்டம் கணக்கீடுகளைச் செய்வதற்கான ஒரு SDK ஆகும், இது இந்த குவாண்டம் இயந்திரக் கொள்கைகளைப் பயன்படுத்துகிறது குவாண்டம் சர்க்யூட்கள். குவாண்டம் கேட்கள், அறிவுறுத்தல்கள் மற்றும் கிளாசிக்கல் கட்டுப்பாட்டு தர்க்கம் ஆகியவற்றைக் கொண்ட குவாண்டம் சர்க்யூட்கள் சிக்கலான வழிமுறைகளையும் பயன்பாடுகளையும் ஒரு குவாண்டம் கணினியில் செயல்படுத்தக்கூடிய சுருக்க முறையில் வெளிப்படுத்த அனுமதிக்கின்றன. அதன் மையத்தில், Qiskit என்பது ஒரு குவாண்டம் சர்க்யூட் கட்டுமானம், தேர்வுமுறை மற்றும் செயல்படுத்தல் இயந்திரம். கூடுதல் வழிமுறை மற்றும் பயன்பாட்டு அடுக்குகள் குவாண்டம் சர்க்யூட்களை, பெரும்பாலும் கிளாசிக்கல் கம்ப்யூட்டிங் ஆதாரங்களுடன் இணைந்து, தேர்வுமுறை, குவாண்டம் வேதியியல், இயற்பியல், இயந்திர கற்றல் மற்றும் நிதி ஆகியவற்றில் சிக்கல்களைத் தீர்க்கின்றன. பின்வருவனவற்றில், குவாண்டம் கம்ப்யூட்டிங் பற்றிய மிகச் சுருக்கமான கண்ணோட்டத்தையும், ஒவ்வொரு அடியிலும் qiskit எவ்வாறு பயன்படுத்தப்படுகிறது என்பதையும் தருகிறோம். ஆர்வமுள்ள வாசகர்கள் கூடுதல் நுண்ணறிவுகளுக்கும், கூடுதல் ஆழமான பொருட்களுக்கும் அனுப்பப்படுகிறார்கள்.
குறுக்கீடு#
கிளாசிக்கல் கணினியைப் போலவே, ஒரு குவாண்டம் கணினி பிட்கள் மூலமாகவே இயங்குகின்றன. எனினும், கிளாசிக்கல் பிட்களை 0 மற்றும் 1 நிலைகளில் மட்டுமே காண முடியும், ஒரு குவாண்டம் பிட் அல்லது க்யூபிட், 0 மற்றும் 1 மதிப்புகளை அல்லது இரண்டின் நேரியல் சேர்க்கைகளையும் குறிக்க முடியும். இந்த நேரியல் சேர்க்கைகள் சூப்பர்பொசிஷன்கள் (அல்லது சூப்பர்பொசிஷன் நிலைகள்) என்று அழைக்கப்படுகின்றன.
குவாண்டம் கணக்கீட்டில் இந்த ஆதாரம் எவ்வாறு பயன்படுத்தப்படுகிறது என்பதைப் பார்க்க, நாம் முதலில் ஒரு கிளாசிக்கல் அனலாக்: சத்தம் ரத்து. சத்தம் ரத்துசெய்தல், எடுத்துக்காட்டாக, சத்தம் ரத்துசெய்யும் ஹெட்ஃபோன்களில் செய்யப்படுவது போல, ஏறக்குறைய ஒரே அதிர்வெண் மற்றும் அலைவீச்சின் தொனியை உருவாக்குவதன் மூலம் தேவையற்ற சத்தத்தின் வீச்சைக் குறைக்க சூப்பர்பொசிஷன் மற்றும் interference என்ற கொள்கையைப் பயன்படுத்துவதன் மூலம் செய்யப்படுகிறது, ஆனால் கட்டத்திற்கு வெளியே இதன் மதிப்பு \(\pi\) (அல்லது வேறு ஏதேனும் ஒற்றைப்படை முழு எண் \(\pi\)).
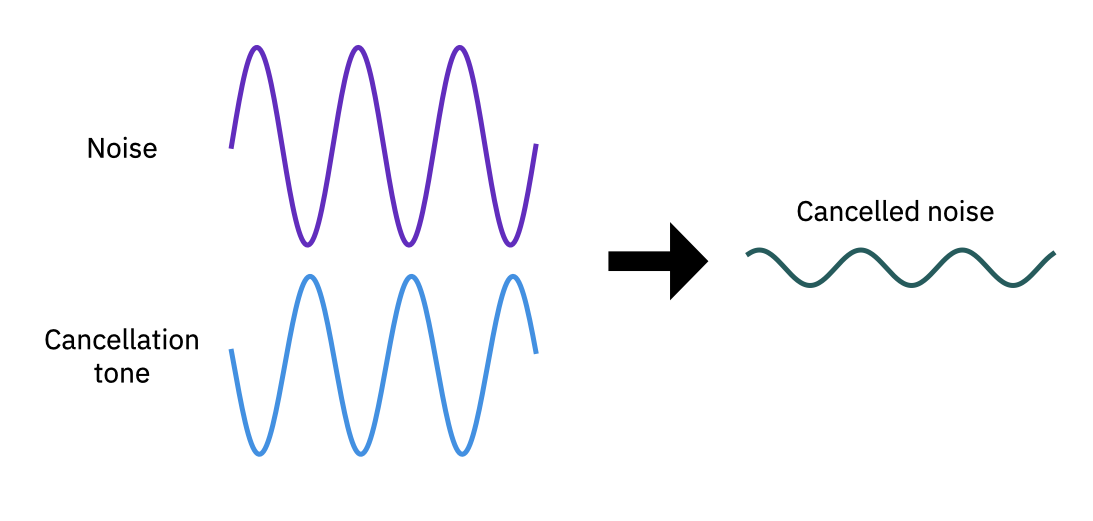
Fig. 1 ஒரு noise சிக்னல் தோராயமான ரத்து கிட்டத்தட்ட சமமான வீச்சு மற்றும் ஒரு கட்டத்தால் ஈடுசெய்யப்படுகிறது \(\sim \pi\).#
மேலே காட்டப்பட்டுள்ளபடி, பக்க வித்தியாசம் \(\pi\) இன் ஒற்றைப்படை மடங்குக்கு நெருக்கமாக இருக்கும்போது, இரண்டு அலைகளின் சூப்பர் பொசிஷன் குறுக்கீட்டில் விளைகிறது, மேலும் அசலுடன் ஒப்பிடும்போது ஒரு வெளியீடு கணிசமாகக் குறைக்கப்படுகிறது. இதன் விளைவாக இரைச்சலால் பாதிக்கப்படாத சிக்னல் ஆஃப் இண்ட்ரஸ்ட் வெளியாகிறது. இந்த செயலாக்கம் டிஜிட்டல் சர்க்யூட்களால் செய்யப்படுகிறது என்றாலும், வீச்சு மற்றும் கட்டம் தொடர்ச்சியான மாறிகள், அவை ஒருபோதும் சரியாக பொருந்தாது, இதன் விளைவாக முழுமையற்ற திருத்தம் ஏற்படுகிறது.
ஒரு குவாண்டக் கணினியில் ஒரு பொதுவான கணக்கீடு சத்தம் ரத்துசெய்யப்படுவதைப் போலவே தொடர்கிறது. ஒரு வேலை தொடங்குவதற்காக, ஒருவர் அணைத்து கணக்கீட்டு நிலைகளுக்கும் ஒரு சூப்பர்பொசிஷனை தயாரிக்கிறார். இது பின்னர் ஒரு உள்ளீடாக quantum circuit ஒரு குறிப்பிட்ட வழிமுறையின்படி சூப்பர்பொசிஷனின் கூறுகளைத் தேர்ந்தெடுக்கப் பயன்படுத்தப்படுகிறது. உள்ளீட்டு நிலையின் ஒப்பீட்டு வீச்சுகள் மற்றும் கட்டங்களை ரத்துசெய்த பிறகு எஞ்சியிருப்பது குவாண்டம் சுற்று மூலம் நிகழ்த்தப்படும் கணக்கீட்டிற்கான தீர்வாகும்.
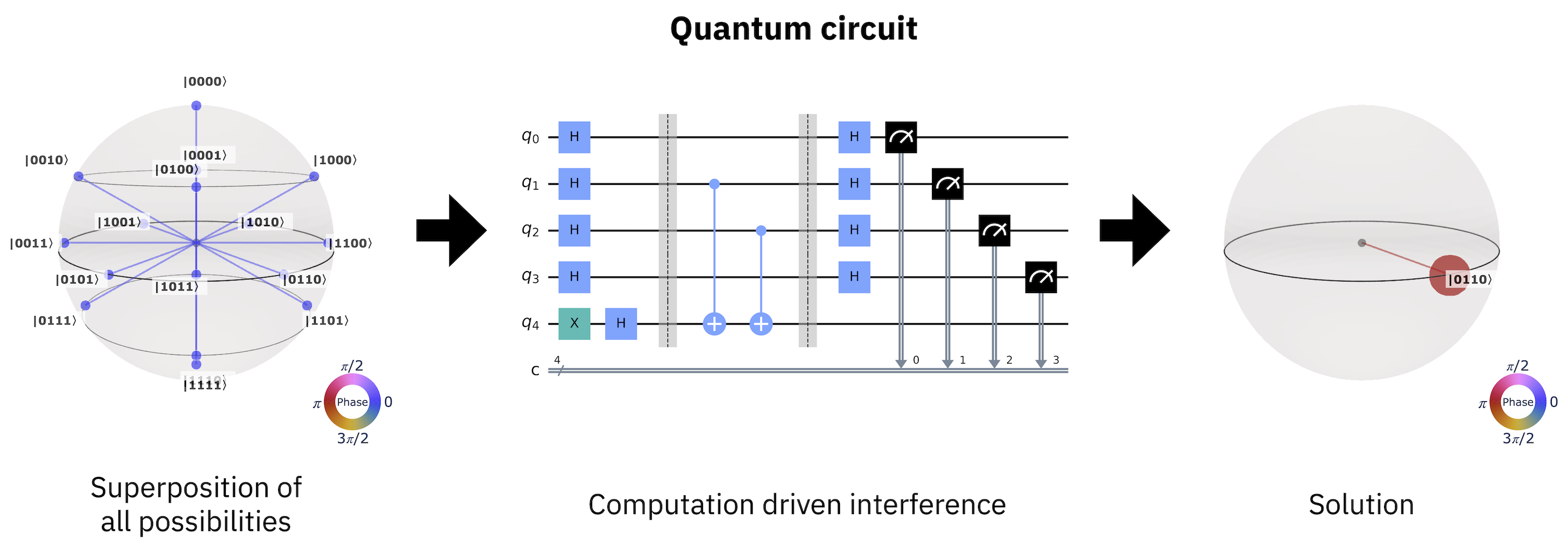
Fig. 2 குறுக்கீடு உருவாக்கும் செயல்முறையாக குவாண்டம் கணக்கீடு.#
என்டான்கில்மெண்ட்#
குவாண்டம் கணக்கீடு பயன்படுத்தக்கூடிய குவாண்டம் இயக்கவியலின் இரண்டாவது கொள்கை நிகழ்வுகளாக entanglement அமையும். என்டான்கில்மெண்ட் ஒன்றுக்கு மேற்பட்ட க்யூபிட் நிலைகளைக்(அல்லது பொதுவாக துகள்கள்) குறிப்பிடுகிறது, இதில் க்யூபிட்களின் ஒருங்கிணைந்த நிலை க்யூபிட்கள் சுயாதீனமாக செய்வதை விட அதிகமான தகவல்களைக் கொண்டுள்ளது. பல-க்யூபிட் குவாண்டம் நிலைகளில் பெரும்பான்மையானவை என்டான்கில்ட், மதிப்புமிக்க வளத்தைக் குறிக்கின்றன. எடுத்துக்காட்டாக, க்யூபிட்களுக்கு இடையில் சிக்கித் தவிக்கும் நிலைகள் குவாண்டம் டெலிபோர்ட்டேஷனுக்குப் பயன்படுத்தப்படலாம், அங்கு இரண்டு க்யூபிட்களின் பகிரப்பட்ட என்டான்கில்ட் நிலையை ஒரு க்யூபிட்லிருந்து இன்னொரு இடத்திற்கு மாற்றுவதற்கு கையாளலாம், இது க்யூபிட்களின் ஒப்பீட்டு உடல் அருகாமையைப் பொருட்படுத்தாமல். குவாண்டம் அமைப்புகளின் இயற்கையான நிலைகளாக, என்டான்கில்ட் நிலைகள், குவாண்டம் வேதியியல் மற்றும் குவாண்டம் உருவகப்படுத்துதல் போன்ற துறைகளிலும் முக்கியத்துவம் வாய்ந்தவை, அங்கு தீர்வு(கள்) பெரும்பாலும் என்டான்கில்ட் பல க்யூபிட் நிலைகளின் வடிவத்தை எடுக்கும். ஒருவர் பல க்யூபிட்களின் அதிக என்டான்கில்ட் குவாண்டம் நிலைகளையும் பயன்படுத்தலாம், எடுத்துக்காட்டாக, சான்றளிக்கும் வகையில் சீரற்ற எண்களை உருவாக்கலாம். இதனைச் செய்ய ஒரு Qiskit package கூட உள்ளது!
குவாண்டம் சர்க்யூட்கள்#
குவாண்டம் இயந்திர வளங்களைப் பயன்படுத்தும் வழிமுறைகள் மற்றும் பயன்பாடுகளை எளிதாகவும் திறமையாகவும் quantum circuits மொழியில் எழுதலாம். ஒரு குவாண்டம் சர்க்யூட் என்பது குவாண்டம் தரவுகளில் ஒத்திசைவான குவாண்டம் செயல்பாடுகளை உள்ளடக்கிய ஒரு கணக்கீட்டு வழக்கமாகும், அதாவது க்யூபிட்ல் நடத்தப்பட்டவை, மற்றும் ஒரே நேரத்தில் நிகழ்நேர கிளாசிக்கல் கணக்கீடு ஆகும். ஒவ்வொரு கிடைமட்டக் கோடு, அல்லது ஒரு சுற்றில் உள்ள கம்பி ஒரு க்யூபிட்டைக் குறிக்கிறது. கம்பியின் இடது முனை ஆரம்ப குவாண்டம் தரவு, மற்றும் வலது குவாண்டம் சர்க்யூட்டின் கணக்கீட்டால் உருவாக்கப்படும் இறுதி குவாண்டம் தரவு. க்யூபிட்களில் செயல்பாடுகள் இந்த கம்பிகளில் வைக்கப்படலாம், மேலும் அவை பெட்டிகளால் குறிக்கப்படுகின்றன.
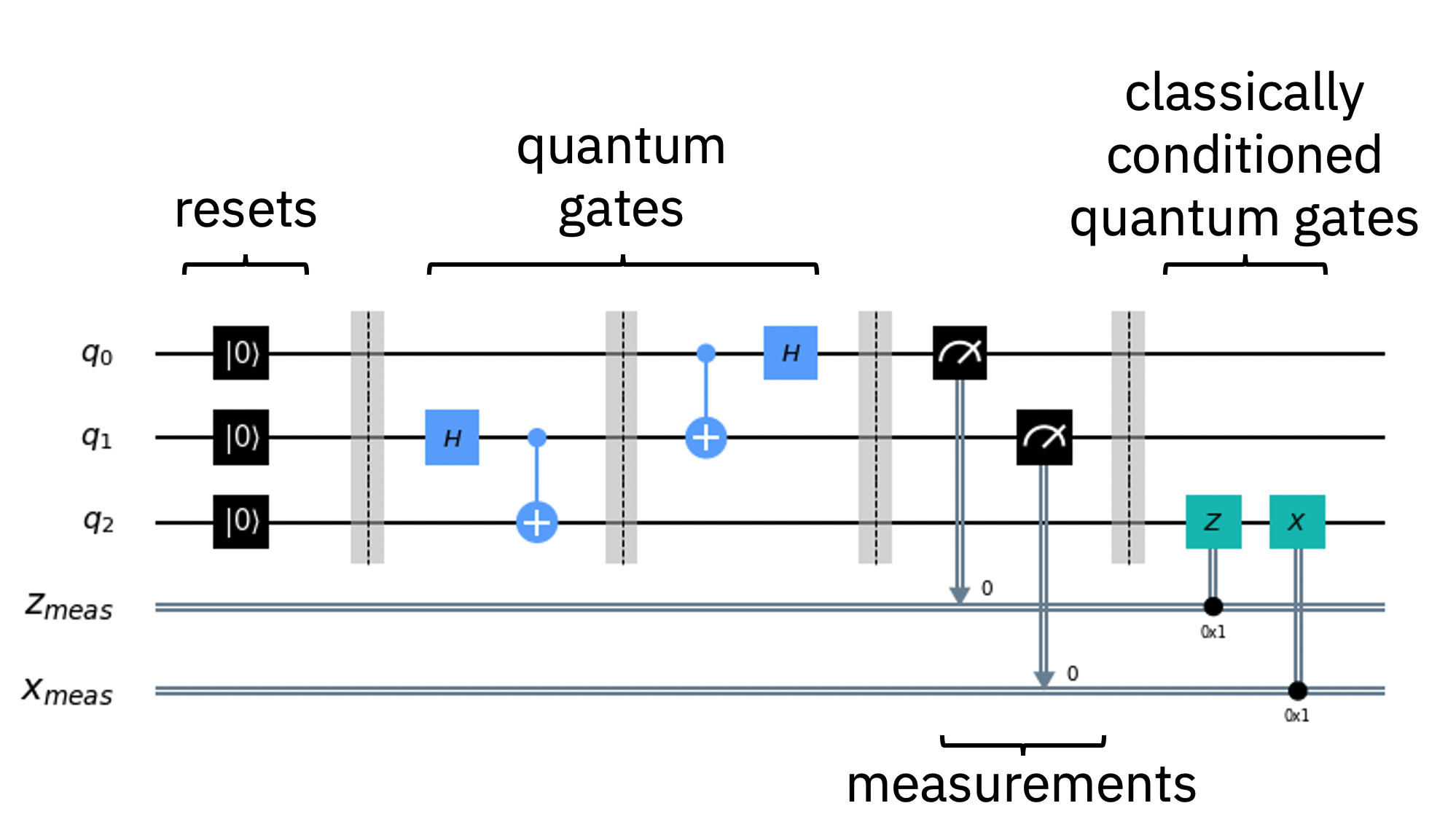
Fig. 3 குவாண்டம் நிலை டெலிபோர்ட்டேஷன் சர்க்யூட் மறுபார்வை.#
குவாண்டம் சுற்றுகள் ஒரு குவாண்டம் கணினியை கிளாசிக்கல் தகவல்களை எடுத்து கிளாசிக்கல் தீர்வை வெளியிடுவதற்கு உதவுகின்றன. இது interference மற்றும் entanglement க்கு கணக்கீடு செய்ய உதவுவதன் மூலம், குவாண்டம் கொள்கைகளை மேம்படுத்துகிறது.
ஒரு பொதுவான குவாண்டம் வழிமுறை பணிப்பாய்வு பின்வருமாறு:
நாம் தீர்க்க விரும்பும் பிரச்சினை,
ஒரு குவாண்டம் சர்க்யூட் பற்றிய விளக்கத்தை உருவாக்கும் ஒரு கிளாசிக்கல் வழிமுறை,
குவாண்டம் வன்பொருளில் இயக்கப்பட வேண்டிய குவாண்டம் சர்க்யூட்,
அது உருவாக்கும் சிக்கலுக்கு வெளியாகும் கிளாசிக்கல் தீர்வு.
குவாண்டம் கேட்ஸ் குவாண்டம் தரவின் பழமையான செயல்பாடுகளை உருவாக்குகிறது. குவாண்டம் கேட்ஸ் தகவல் பாதுகாத்தல், க்விட்களில் சேமிக்கப்பட்ட குவாண்டம் தரவின் மீளக்கூடிய மாற்றங்கள் ஆகியவற்றைக் குறிக்கிறது. இந்த "ஒற்றை" மாற்றங்கள் குவாண்டம் சுற்றின் குவாண்டம் இயந்திர மையத்தைக் குறிக்கின்றன. \(X\) (\(\oplus\) என்றும் எழுதப்பட்டுள்ளது) மற்றும் \(CX\) ஆனது முறையே பிட்-ஃபிளிப் மற்றும் \(XOR\) செயல்பாடுகள், முறையே, மற்றவை இல்லை. ஹடாமார்ட் (\(H\)) வாயிலுடன், அளவுரு சுழற்சி சுழல்கிறது \(rX(\theta)\) மற்றும் \(rY(\theta)\), வாயில்கள் \(Z\), \(rZ(\theta)\), \(S\), மற்றும் \(T\) குறுக்கீட்டிற்குப் பயன்படுத்தக்கூடிய கட்டங்களை வழங்குகிறது இரண்டு-க்விட் வாயில்கள் \(CX\) கேட் ஜோடி க்விட்களுக்கு இடையில் சிக்கலை உருவாக்க பயன்படுகிறது, அல்லது கட்டத்தை ஒரு குவிட்டில் இருந்து இன்னொரு கட்டத்திற்கு" உதைக்க "பயன்படுகிறது. வாயில்களுக்கு மாறாக, "அளவீடு" போன்ற செயல்பாடுகள், ஒரு "இலக்கு" கம்பியுடன் இணைக்கும் ஒரு கோடுடன் ஒரு பெட்டியில் மீட்டர் குறியீட்டால் குறிப்பிடப்படுகின்றன, ஒரு குவிட் நிலை பற்றிய பகுதியளவு தகவலைப் பிரித்தெடுக்கவும், பெரும்பாலும் கட்டத்தை இழந்து, அதை பிரதிநிதித்துவப்படுத்த முடியும் ஒரு கிளாசிக்கல் பிட் மற்றும் அந்த கிளாசிக்கல் பிட்டை இலக்கு கம்பியில் எழுதுங்கள் (பெரும்பாலும் சில ரீடுஅவுட் சாதனத்தில் ஒரு முழுமையான கிளாசிக்கல் கம்பி). குவாண்டம் தரவிலிருந்து தகவல்களை கிளாசிக்கல் சாதனத்திற்கு எடுத்துச் செல்வதற்கான பொதுவான வழி இது. \(H\), \(rZ(\theta)\), \(CX\), மற்றும் அளவீட்டு வாயில்கள், அதாவது உலகளாவிய வாயில் தொகுப்பு, மற்றும் எந்தவிதமான குவாண்டம் சுற்றையும் உருவாக்கலாம். இதில் அனைத்து இயற்கை இயற்பியல் அமைப்பின் மாற்றங்களைத் திறமையாகக் கணக்கிடுவதும் உட்படும்.
சில பணிச்சுமைகள் இன்டர்லீவ் குவாண்டம் சர்க்யூட்கள் மற்றும் கிளாசிக்கல் கணக்கீட்டின் நீட்டிக்கப்பட்ட வரிசையைக் கொண்டிருக்கின்றன, எடுத்துக்காட்டாக மாறுபட்ட குவாண்டம் வழிமுறைகள் ஒரு தேர்வுமுறை சுழற்சியில் குவாண்டம் சர்க்யூட்களை இயக்குகின்றன. இந்த பணிச்சுமைகளுக்கு, குவாண்டம் சர்க்யூட்கள் அளவுருவாக்கப்பாட்டால் கணினி செயல்திறன் கணிசமாக அதிகரிக்கிறது, மேலும் சர்க்யூட் செயல்படுத்தல் மற்றும் தற்போதைய அல்லாத கிளாசிக்கல் கணக்கீடு ஆகியவற்றுக்கு இடையிலான மாற்றங்கள் திறமையாக செய்யப்படுகின்றன. இதன் விளைவாக, கணக்கீட்டு நேரத்தை விரைவுபடுத்துவதற்காக உருவாக்கப்பட்ட வன்பொருள்களுடன் குவாண்டம் சுற்றுகளை மீண்டும் மீண்டும் பயன்படுத்தும் வழிமுறைகளுடன் கூடிய கணக்கீடுகளைக் குறிக்க near-time computation ஐ வரையறுக்கிறோம். Near-time computation-ல், கிளாசிக்கல் கணக்கீடு, குவாண்டம் கணக்கீட்டின் ஒத்திசைவைக் காட்டிலும் நீண்ட கால இடைவெளியில் நிகழ்கிறது. Real-time computation உடன் இதை வேறுபடுத்துங்கள், அங்கு குவாண்டம் சாதனத்தின் டிகோஹரன்ஸ் நேரத்திற்குள் கிளாசிக்கல் கணக்கீடு நிகழ்கிறது.
குறைந்த முயற்சியுடன் சிக்கலான குவாண்டம் சர்க்யூட்களை உருவாக்குவது Qiskit இன் மையமாக உள்ளது, இது சிறப்பான செயல்பாடுகளை ஆதரிக்கிறது மற்றும் உங்கள் சர்க்யூட்களை quantum கணினிகள் அல்லது கிளாசிக்கல் சிமுலேட்டர்களுக்கு அனுப்பலாம். குறியீட்டின் சில வரிகளை மட்டுமே கொண்டு, மேலே உள்ளதைப் போன்ற சிக்கலான சுற்றுகளை உருவாக்க முடியும்.
qr = QuantumRegister(3, 'q')
cr = ClassicalRegister(2, 'zx_meas')
qc = QuantumCircuit(qr,cr)
qc.reset(range(3))
qc.barrier()
qc.h(1)
qc.cx([1,0],[2,1])
qc.h(0)
qc.barrier()
qc.measure([0,1], [0,1])
qc.barrier()
qc.z(2).c_if(cr, 1)
qc.x(2).c_if(cr, 2)
குவாண்டம் கணினிகள்#

Fig. 4 IBM Quantum System One உள்ளே ஒரு பார்வை.#
குவாண்டம் சர்க்யூட்களைப் பயன்படுத்தி திட்டமிடப்பட்ட குவாண்டம் கணினிகள் குவாண்டம் கூறுகளை வரையறுக்க அனுமதிக்கும் எந்த குவாண்டம் தொழில்நுட்பத்திலிருந்தும் உருவாக்கப்படலாம், மேலும் ஒற்றை மற்றும் பல-க்யூபிட் கேட் செயல்பாடுகளை அதிக நம்பகத்தன்மையுடன் செயல்படுத்த முடியும். தற்போது, சூப்பர் கண்டக்டிங் சர்க்யூட்கள், ட்ராப்ட்-அயனிகள், குறைக்கடத்தி குவாண்டம்-புள்ளிகள், ஃபோட்டான்கள் மற்றும் நடுநிலை அணுக்கள் ஆகியவற்றை அடிப்படையாகக் கொண்ட கட்டமைப்புகள் தீவிரமாக உருவாக்கப்பட்டு வருகின்றன, மேலும் பல இணையத்தில் பயனர்களுக்கு அணுகப்படுகின்றன. கொடுக்கப்பட்ட குவாண்டம் அமைப்பின் அடிப்படைக் கட்டமைப்பைப் பொறுத்தவரை Qiskit அஞ்ஞானவாதி, மேலும் ஒரு குவாண்டம் சாதனத்தின் சிக்கலான கேட் டோபாலஜியுடன் பொருந்த ஒரு குவாண்டம் சர்க்யூட்டைத் தொகுக்கலாம், சர்க்யூட் வழிமுறைகளைச் சாதனத்தின் சொந்த கேட் தொகுப்பில் வரைபடமாக்கலாம் மற்றும் அதன் விளைவாக வரும் குவாண்டம் சர்க்யூட்டின் நம்பகத்தன்மையை மேம்படுத்தலாம்.
மேலே உள்ள சத்தம் நீக்குதல் உதாரணத்தைப் போலவே, க்யூபிட்களின் வீச்சு மற்றும் கட்டம் தொடர்ச்சியான சுதந்திரத்தின் அளவுகள் ஆகும், அதன் அடிப்படையில் செயல்பாடுகள் ஒருபோதும் சரியாக செய்ய முடியாது. இந்த கேட் பிழைகள், ஒரு குவாண்டம் கணினி வசிக்கும் சூழலில் இருந்து வரும் சத்தத்துடன், தொகுப்பு செயல்பாட்டில் கணக்கிடப்படாவிட்டால் ஒரு கணக்கீட்டை அழிக்க சதி செய்யலாம், மேலும் இன்றைய நாளில் அதிக நம்பகத்தன்மையை வெளியிடுவதற்கு கூடுதல் தணிப்பு நடைமுறைகள் தேவைப்படலாம், இதனால் குவாண்டம் அமைப்புகள் சத்தத்திற்கு ஆளாகின்றன. Qiskit அதன் தொகுப்பு மூலோபாயத்தில் பரந்த அளவிலான சாதன அளவீட்டு அளவீடுகளை (கீழே உள்ள படத்தைக் காண்க) கணக்கில் எடுத்துக்கொள்ளும் திறன் கொண்டது, மேலும் கொடுக்கப்பட்ட குவாண்டம் சுற்றுவட்டத்தை இயக்குவதற்கான உகந்த தொகுப்புகளை தேர்ந்தெடுக்கலாம். கூடுதலாக, ஒரு குவாண்டம் சர்க்யூட்கள் வெளியீட்டின் உண்மையுள்ள பிரதிநிதித்துவத்தைப் பிரித்தெடுப்பதற்கான சத்தம் குறைப்பு நுட்பங்களின் தொகுப்பை Qiskit வழங்குகிறது.
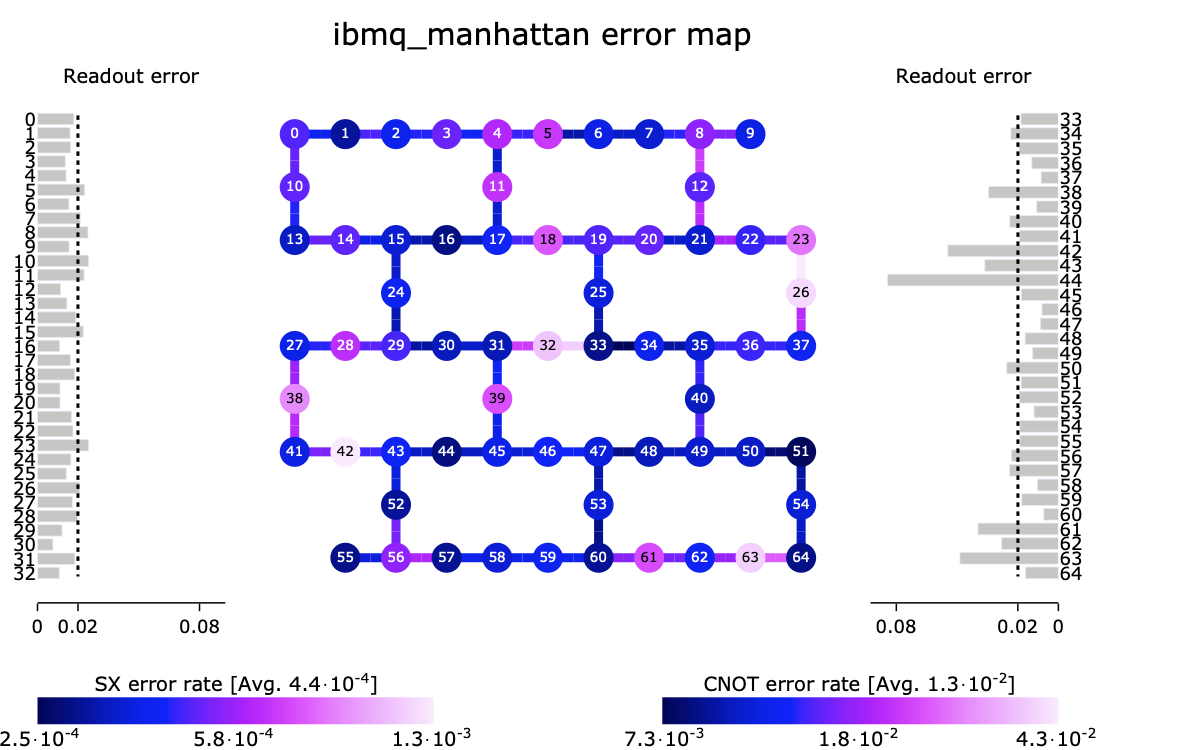
Fig. 5 IBM Quantum ibmq_manhattan system-இன் இடவியல் மற்றும் பிழை விகிதங்கள்.#
இங்கிருந்து எங்கே செல்ல#
குவாண்டம் கணக்கீடு என்ன வழங்க வேண்டும் என்பதற்கான சுவையை வாசகருக்கு நாங்கள் வழங்கியுள்ளோம், மேலும் நீங்கள் பசியுடன் இருக்கிறீர்கள். அப்படியானால், ஆர்வமுள்ள பல ஆதாரங்கள் உள்ளன:
Qiskit-ஐ வைத்துத் தொடங்குதல் - நேரடியாக Qiskit-ற்குள் குதிக்கலாம்.
குவாண்டம் கணினிகளுக்கான கள வழிகாட்டி : குவாண்டம் கணக்கீட்டின் சில நிறுவனர்களால் எழுதப்பட்ட ஒரு மென்மையான இயற்பியல் அடிப்படையிலான அறிமுகம், இது ஊடாடும் சர்க்யூட்டை உருவாக்கப் பயன்படுத்துகிறது.
Qiskit textbook : A university quantum algorithms/computation course supplement based on Qiskit.