FourierChecking#

class qiskit.circuit.library.FourierChecking(f, g)[Quellcode]#

Bases: QuantumCircuit

Fourier checking circuit.

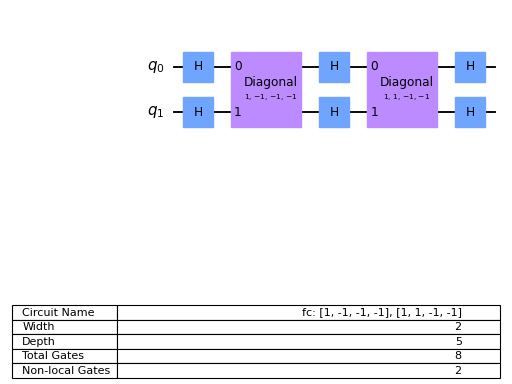
The circuit for the Fourier checking algorithm, introduced in [1], involves a layer of Hadamards, the function \(f\), another layer of Hadamards, the function \(g\), followed by a final layer of Hadamards. The functions \(f\) and \(g\) are classical functions realized as phase oracles (diagonal operators with {-1, 1} on the diagonal).

The probability of observing the all-zeros string is \(p(f,g)\). The algorithm solves the promise Fourier checking problem, which decides if f is correlated with the Fourier transform of g, by testing if \(p(f,g) <= 0.01\) or \(p(f,g) >= 0.05\), promised that one or the other of these is true.

The functions \(f\) and \(g\) are currently implemented from their truth tables but could be represented concisely and implemented efficiently for special classes of functions.

Fourier checking is a special case of \(k\)-fold forrelation [2].

Reference:

[1] S. Aaronson, BQP and the Polynomial Hierarchy, 2009 (Section 3.2). arXiv:0910.4698

[2] S. Aaronson, A. Ambainis, Forrelation: a problem that optimally separates quantum from classical computing, 2014. arXiv:1411.5729

Create Fourier checking circuit.

Parameter:

f (List[int]) – truth table for f, length 2**n list of {1,-1}.
g (List[int]) – truth table for g, length 2**n list of {1,-1}.

Verursacht:

CircuitError – if the inputs f and g are not valid.

Reference Circuit:: (Source code)

Attributes

ancillas#: Returns a list of ancilla bits in the order that the registers were added.

calibrations#

Return calibration dictionary.

The custom pulse definition of a given gate is of the form {'gate_name': {(qubits, params): schedule}}

clbits#: Returns a list of classical bits in the order that the registers were added.

data#

Return the circuit data (instructions and context).

Rückgabe:: a list-like object containing the CircuitInstructions for each instruction.
Rückgabetyp:: QuantumCircuitData

extension_lib = 'include "qelib1.inc";'#

global_phase#: Return the global phase of the circuit in radians.

header = 'OPENQASM 2.0;'#

instances = 137#

layout#

Return any associated layout information about the circuit

This attribute contains an optional TranspileLayout object. This is typically set on the output from transpile() or PassManager.run() to retain information about the permutations caused on the input circuit by transpilation.

There are two types of permutations caused by the transpile() function, an initial layout which permutes the qubits based on the selected physical qubits on the Target, and a final layout which is an output permutation caused by SwapGates inserted during routing.

metadata#

The user provided metadata associated with the circuit.

The metadata for the circuit is a user provided dict of metadata for the circuit. It will not be used to influence the execution or operation of the circuit, but it is expected to be passed between all transforms of the circuit (ie transpilation) and that providers will associate any circuit metadata with the results it returns from execution of that circuit.

num_ancillas#: Return the number of ancilla qubits.

num_clbits#: Return number of classical bits.

num_parameters#: The number of parameter objects in the circuit.

num_qubits#: Return number of qubits.

op_start_times#

Return a list of operation start times.

This attribute is enabled once one of scheduling analysis passes runs on the quantum circuit.

Rückgabe:: List of integers representing instruction start times. The index corresponds to the index of instruction in QuantumCircuit.data.
Verursacht:: AttributeError – When circuit is not scheduled.

parameters#

The parameters defined in the circuit.

This attribute returns the Parameter objects in the circuit sorted alphabetically. Note that parameters instantiated with a ParameterVector are still sorted numerically.

Examples

The snippet below shows that insertion order of parameters does not matter.

>>> from qiskit.circuit import QuantumCircuit, Parameter
>>> a, b, elephant = Parameter("a"), Parameter("b"), Parameter("elephant")
>>> circuit = QuantumCircuit(1)
>>> circuit.rx(b, 0)
>>> circuit.rz(elephant, 0)
>>> circuit.ry(a, 0)
>>> circuit.parameters  # sorted alphabetically!
ParameterView([Parameter(a), Parameter(b), Parameter(elephant)])

Bear in mind that alphabetical sorting might be unintuitive when it comes to numbers. The literal „10“ comes before „2“ in strict alphabetical sorting.

>>> from qiskit.circuit import QuantumCircuit, Parameter
>>> angles = [Parameter("angle_1"), Parameter("angle_2"), Parameter("angle_10")]
>>> circuit = QuantumCircuit(1)
>>> circuit.u(*angles, 0)
>>> circuit.draw()
   ┌─────────────────────────────┐
q: ┤ U(angle_1,angle_2,angle_10) ├
   └─────────────────────────────┘
>>> circuit.parameters
ParameterView([Parameter(angle_1), Parameter(angle_10), Parameter(angle_2)])

To respect numerical sorting, a ParameterVector can be used.

>>> from qiskit.circuit import QuantumCircuit, Parameter, ParameterVector
>>> x = ParameterVector("x", 12)
>>> circuit = QuantumCircuit(1)
>>> for x_i in x:
...     circuit.rx(x_i, 0)
>>> circuit.parameters
ParameterView([
    ParameterVectorElement(x[0]), ParameterVectorElement(x[1]),
    ParameterVectorElement(x[2]), ParameterVectorElement(x[3]),
    ..., ParameterVectorElement(x[11])
])

Rückgabe:: The sorted Parameter objects in the circuit.

prefix = 'circuit'#

qubits#: Returns a list of quantum bits in the order that the registers were added.