Note
This page was generated from tutorials/algorithms/06_qaoa.ipynb.
Run interactively in the IBM Quantum lab.
Quantum Approximate Optimization Algorithm¶
Qiskit has an implementation of the Quantum Approximate Optimization Algorithm QAOA and this notebook demonstrates using it for a graph partition problem.
While QAOA can be directly used it often more convenient to use it in conjunction with the Optimization module. See the Optimization tutorials for more information.
[1]:
import numpy as np
import networkx as nx
from qiskit import BasicAer
from qiskit.aqua.algorithms import NumPyMinimumEigensolver
from qiskit.optimization.applications.ising import graph_partition
from qiskit.optimization.applications.ising.common import random_graph, sample_most_likely
/home/computertreker/git/qiskit/qiskit-dup/.tox/docs/lib/python3.7/site-packages/qiskit/optimization/__init__.py:92: DeprecationWarning: The package qiskit.optimization is deprecated. It was moved/refactored to qiskit_optimization (pip install qiskit-optimization). For more information see <https://github.com/Qiskit/qiskit-aqua/blob/master/README.md#migration-guide>
warn_package('optimization', 'qiskit_optimization', 'qiskit-optimization')
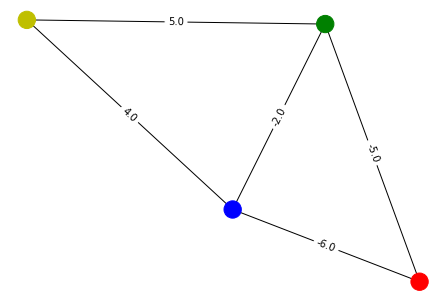
First we create a random graph and draw it so it can be seen.
[2]:
num_nodes = 4
w = random_graph(num_nodes, edge_prob=0.8, weight_range=10, seed=48)
print(w)
[[ 0. -5. -6. 0.]
[-5. 0. -2. 5.]
[-6. -2. 0. 4.]
[ 0. 5. 4. 0.]]
/home/computertreker/git/qiskit/qiskit-dup/.tox/docs/lib/python3.7/site-packages/qiskit/optimization/applications/ising/common.py:42: DeprecationWarning: The variable qiskit.aqua.aqua_globals is deprecated. It was moved/refactored to qiskit.utils.algorithm_globals (pip install qiskit-terra). For more information see <https://github.com/Qiskit/qiskit-aqua/blob/master/README.md#migration-guide>
aqua_globals.random_seed = seed
[3]:
G = nx.from_numpy_matrix(w)
layout = nx.random_layout(G, seed=10)
colors = ['r', 'g', 'b', 'y']
nx.draw(G, layout, node_color=colors)
labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos=layout, edge_labels=labels);
[3]:
{(0, 1): Text(0.7024844288825989, 0.3847779016941786, '-5.0'),
(0, 2): Text(0.634913831949234, 0.12277430109679699, '-6.0'),
(1, 2): Text(0.5660776197910309, 0.48680025339126587, '-2.0'),
(1, 3): Text(0.4158555418252945, 0.7546672821044922, '5.0'),
(2, 3): Text(0.3482849448919296, 0.4926636815071106, '4.0')}
The brute-force method is as follows. Basically, we exhaustively try all the binary assignments. In each binary assignment, the entry of a vertex is either 0 (meaning the vertex is in the first partition) or 1 (meaning the vertex is in the second partition). We print the binary assignment that satisfies the definition of the graph partition and corresponds to the minimal number of crossing edges.
[4]:
def brute_force():
# use the brute-force way to generate the oracle
def bitfield(n, L):
result = np.binary_repr(n, L)
return [int(digit) for digit in result] # [2:] to chop off the "0b" part
L = num_nodes
max = 2**L
minimal_v = np.inf
for i in range(max):
cur = bitfield(i, L)
how_many_nonzero = np.count_nonzero(cur)
if how_many_nonzero * 2 != L: # not balanced
continue
cur_v = graph_partition.objective_value(np.array(cur), w)
if cur_v < minimal_v:
minimal_v = cur_v
return minimal_v
sol = brute_force()
print(f'Objective value computed by the brute-force method is {sol}')
Objective value computed by the brute-force method is 3
The graph partition problem can be converted to an Ising Hamiltonian. Qiskit has different capabilities in the Optimization module to do this. Here, since the goal is to show QAOA, the module is used without further explanation to create the operator. The paper Ising formulations of many NP problems may be of interest if you would like to understand the technique further.
[5]:
qubit_op, offset = graph_partition.get_operator(w)
/home/computertreker/git/qiskit/qiskit-dup/.tox/docs/lib/python3.7/site-packages/qiskit/optimization/applications/ising/graph_partition.py:72: DeprecationWarning: The package qiskit.aqua.operators is deprecated. It was moved/refactored to qiskit.opflow (pip install qiskit-terra). For more information see <https://github.com/Qiskit/qiskit-aqua/blob/master/README.md#migration-guide>
return WeightedPauliOperator(paulis=pauli_list), shift
So lets use the QAOA algorithm to find the solution.
[6]:
from qiskit.aqua import aqua_globals
from qiskit.aqua.algorithms import QAOA
from qiskit.aqua.components.optimizers import COBYLA
from qiskit.circuit.library import TwoLocal
aqua_globals.random_seed = 10598
optimizer = COBYLA()
qaoa = QAOA(qubit_op, optimizer, quantum_instance=BasicAer.get_backend('statevector_simulator'))
result = qaoa.compute_minimum_eigenvalue()
x = sample_most_likely(result.eigenstate)
ising_sol = graph_partition.get_graph_solution(x)
print(ising_sol)
print(f'Objective value computed by QAOA is {graph_partition.objective_value(x, w)}')
/home/computertreker/git/qiskit/qiskit-dup/.tox/docs/lib/python3.7/site-packages/qiskit/aqua/components/optimizers/optimizer.py:50: DeprecationWarning: The package qiskit.aqua.components.optimizers is deprecated. It was moved/refactored to qiskit.algorithms.optimizers (pip install qiskit-terra). For more information see <https://github.com/Qiskit/qiskit-aqua/blob/master/README.md#migration-guide>
'qiskit.algorithms.optimizers', 'qiskit-terra')
/home/computertreker/git/qiskit/qiskit-dup/.tox/docs/lib/python3.7/site-packages/qiskit/aqua/algorithms/vq_algorithm.py:72: DeprecationWarning: The class qiskit.aqua.algorithms.VQAlgorithm is deprecated. It was moved/refactored to qiskit.algorithms.VariationalAlgorithm (pip install qiskit-terra). For more information see <https://github.com/Qiskit/qiskit-aqua/blob/master/README.md#migration-guide>
'qiskit-terra')
/home/computertreker/git/qiskit/qiskit-dup/.tox/docs/lib/python3.7/site-packages/qiskit/aqua/quantum_instance.py:137: DeprecationWarning: The class qiskit.aqua.QuantumInstance is deprecated. It was moved/refactored to qiskit.utils.QuantumInstance (pip install qiskit-terra). For more information see <https://github.com/Qiskit/qiskit-aqua/blob/master/README.md#migration-guide>
'qiskit-terra')
/home/computertreker/git/qiskit/qiskit-dup/.tox/docs/lib/python3.7/site-packages/qiskit/aqua/components/variational_forms/variational_form.py:48: DeprecationWarning: The package qiskit.aqua.components.variational_forms is deprecated. For more information see <https://github.com/Qiskit/qiskit-aqua/blob/master/README.md#migration-guide>
warn_package('aqua.components.variational_forms')
[0. 0. 1. 1.]
Objective value computed by QAOA is 3.0
The outcome can be seen to match to the value computed above by brute force. But we can also use the classical NumPyMinimumEigensolver to do the computation, which may be useful as a reference without doing things by brute force.
[7]:
npme = NumPyMinimumEigensolver(qubit_op)
result = npme.compute_minimum_eigenvalue()
x = sample_most_likely(result.eigenstate)
ising_sol = graph_partition.get_graph_solution(x)
print(ising_sol)
print(f'Objective value computed by the NumPyMinimumEigensolver is {graph_partition.objective_value(x, w)}')
[0 0 1 1]
Objective value computed by the NumPyMinimumEigensolver is 3
/home/computertreker/git/qiskit/qiskit-dup/.tox/docs/lib/python3.7/site-packages/qiskit/aqua/algorithms/minimum_eigen_solvers/minimum_eigen_solver.py:38: DeprecationWarning: The package qiskit.aqua.algorithms.minimum_eigen_solvers is deprecated. It was moved/refactored to qiskit.algorithms.minimum_eigen_solvers (pip install qiskit-terra). For more information see <https://github.com/Qiskit/qiskit-aqua/blob/master/README.md#migration-guide>
'qiskit-terra')
/home/computertreker/git/qiskit/qiskit-dup/.tox/docs/lib/python3.7/site-packages/qiskit/aqua/algorithms/eigen_solvers/eigen_solver.py:38: DeprecationWarning: The package qiskit.aqua.algorithms.eigen_solvers is deprecated. It was moved/refactored to qiskit.algorithms.eigen_solvers (pip install qiskit-terra). For more information see <https://github.com/Qiskit/qiskit-aqua/blob/master/README.md#migration-guide>
'qiskit-terra')
It is also possible to use VQE as is shown below
[8]:
from qiskit.aqua.algorithms import VQE
from qiskit.circuit.library import TwoLocal
aqua_globals.random_seed = 10598
optimizer = COBYLA()
var_form = TwoLocal(qubit_op.num_qubits, 'ry', 'cz', reps=5, entanglement='linear')
vqe = VQE(qubit_op, var_form, optimizer, quantum_instance=BasicAer.get_backend('statevector_simulator'))
result = vqe.compute_minimum_eigenvalue()
x = sample_most_likely(result.eigenstate)
ising_sol = graph_partition.get_graph_solution(x)
print(ising_sol)
print(f'Objective value computed by VQE is {graph_partition.objective_value(x, w)}')
[0. 1. 0. 1.]
Objective value computed by VQE is 3.0
[9]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
| Qiskit | 0.25.4 |
| Terra | 0.17.2 |
| Aer | 0.8.2 |
| Ignis | 0.6.0 |
| Aqua | 0.9.1 |
| IBM Q Provider | 0.12.3 |
| System information | |
| Python | 3.7.7 (default, Apr 22 2020, 19:15:10) [GCC 9.3.0] |
| OS | Linux |
| CPUs | 32 |
| Memory (Gb) | 125.71903228759766 |
| Tue May 25 16:11:59 2021 EDT | |
This code is a part of Qiskit
© Copyright IBM 2017, 2021.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.