Note

Cette page a été générée à partir de tutorials/chemistry/03_ground_state_solvers.ipynb.

Exécuter en mode interactif dans le `IBM Quantum lab <https://quantum-computing.ibm.com/jupyter/tutorial/chemistry/03_ground_state_solvers.ipynb>_.

Solveurs d’état au sol (Ground State Solvers)

Introduction

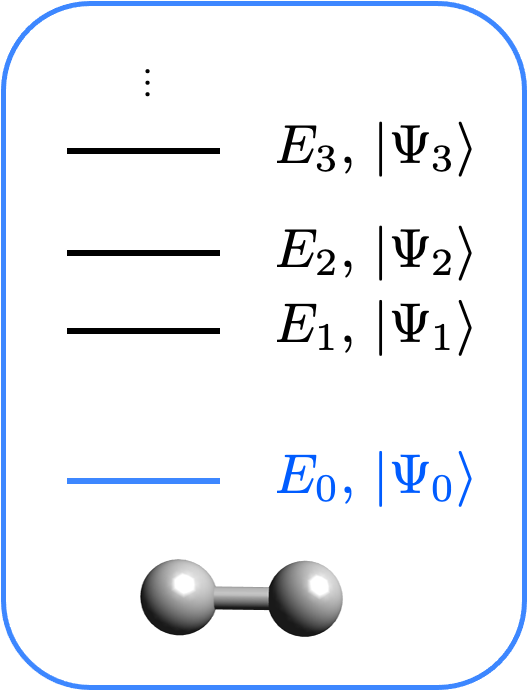
Dans ce tutoriel, nous allons discuter de l’interface pour le calcul de l’état fondamental avec Qiskit Chemistry. L’objectif est de calculer l’état fondamental d’un hamiltonien moléculaire. Cet hamiltonien peut être électronique ou vibronique. Pour en savoir plus sur la préparation de l’hamiltonien, consultez les tutoriels de la structure électronique et les tutoriels de la structure vibronique.

La première étape consiste à définir le système moléculaire. Dans se qui suit, nous demandons la partie électronique d’une molécule d’hydrogène.

from qiskit.chemistry.drivers import PySCFDriver, UnitsType, Molecule
from qiskit.chemistry.transformations import FermionicTransformation, FermionicQubitMappingType

molecule = Molecule(geometry=[['H', [0., 0., 0.]],
                              ['H', [0., 0., 0.735]]],
                     charge=0, multiplicity=1)
driver = PySCFDriver(molecule = molecule, unit=UnitsType.ANGSTROM, basis='sto3g')
transformation = FermionicTransformation(qubit_mapping=FermionicQubitMappingType.JORDAN_WIGNER)

Le Solveur (The Solver)

Ensuite, nous devons définir un solveur (Solver) : le solveur est l’algorithme par lequel l’état du sol (Ground State) est calculé.

Let’s first start with a purely classical example: the NumPy minimum eigensolver. This algorithm exactly diagonalizes the Hamiltonian. Although it scales badly, it can be used on small systems to check the results of the quantum algorithms.

from qiskit.aqua.algorithms import NumPyMinimumEigensolver

numpy_solver = NumPyMinimumEigensolver()

Pour trouver l’état fondamental (Ground State), nous utilisons également l’algorithme Variational Quantum Eigensolver (VQE). Les algorithmes VQE fonctionnent en échangeant des informations entre un ordinateur classique et un ordinateur quantique, tel que décrit dans la figure suivante.

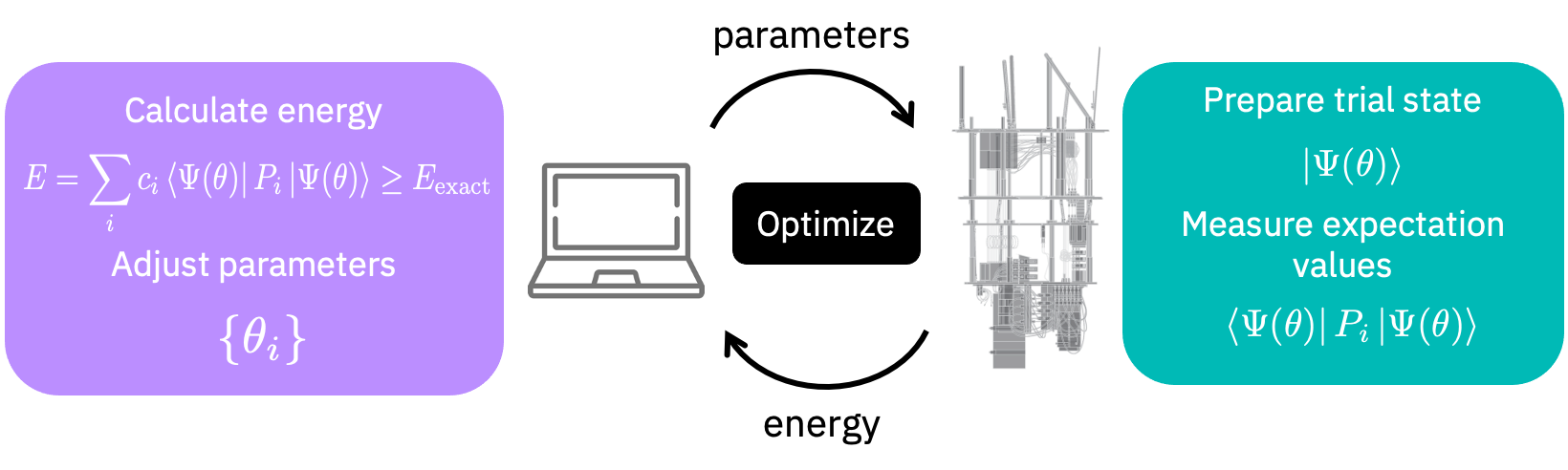
Initialisons un solveur VQE.

from qiskit import BasicAer
from qiskit.aqua import QuantumInstance
from qiskit.chemistry.algorithms.ground_state_solvers.minimum_eigensolver_factories import VQEUCCSDFactory

vqe_solver = VQEUCCSDFactory(QuantumInstance(BasicAer.get_backend('statevector_simulator')))

Pour définir le solveur VQE on a besoin de deux éléments essentiels :

1. Une forme variationnelle : ici nous utilisons l’ansatz Unitary Coupled Cluster (UCC) (voir par exemple [Physical Review A 98,2 (2018): 022322]). Comme il s’agit d’un standard chimique, une manufacture est déjà disponible, permettant une initialisation rapide d’un VQE avec UCC. La valeur par défaut est d’utiliser toutes les excitations simples et doubles, mais le type d’excitation (S, D, SD) ainsi que d’autres paramètres peuvent être sélectionnés.

2. Un état initial : l’état initial des qubits. Dans la manufacture utilisée ci-dessus, les qubits sont initialisés dans le Hartree-Fock (voir le tutoriel de la structure électronique) état initial (les qubits correspondant aux MOs occupés sont \(|1\rangle\) et ceux correspondant aux MOs virtuels sont \(|0\rangle\).

3. Le backend (Backend): c’est la machine quantique sur laquelle la partie droite de la figure ci-dessus sera effectuée. Ici nous demandons l’émulateur quantique parfait (` ` statevector_simulateur ` `).

On pourrait aussi utiliser n’importe quelle forme variationnelle disponible / état initial, ou même définir sa/son propre. Par exemple,

from qiskit.aqua.algorithms import VQE
from qiskit.circuit.library import TwoLocal

num_qubits = 4
tl_circuit = TwoLocal(num_qubits, ['h', 'rx'], 'cz',
                      entanglement='full', reps=3, parameter_prefix = 'y')

tl_circuit.draw(output = 'mpl')

another_solver = VQE(var_form = tl_circuit,
                     quantum_instance = QuantumInstance(BasicAer.get_backend('statevector_simulator')))

Le calcul et les résultats

Nous sommes maintenant prêts à effectuer le calcul.

from qiskit.chemistry.algorithms.ground_state_solvers import GroundStateEigensolver

calc = GroundStateEigensolver(transformation, vqe_solver)
res = calc.solve(driver)

print(res)

=== GROUND STATE ENERGY ===

* Electronic ground state energy (Hartree): -1.857275030145
  - computed part:      -1.857275030145
  - frozen energy part: 0.0
  - particle hole part: 0.0
~ Nuclear repulsion energy (Hartree): 0.719968994449
> Total ground state energy (Hartree): -1.137306035696

=== MEASURED OBSERVABLES ===

  0:  # Particles: 2.000 S: 0.000 S^2: 0.000 M: 0.000

=== DIPOLE MOMENTS ===

~ Nuclear dipole moment (a.u.): [0.0  0.0  1.3889487]

  0:
  * Electronic dipole moment (a.u.): [0.0  0.0  1.38894909]
    - computed part:      [0.0  0.0  1.38894909]
    - frozen energy part: [0.0  0.0  0.0]
    - particle hole part: [0.0  0.0  0.0]
  > Dipole moment (a.u.): [0.0  0.0  -0.00000039]  Total: 0.00000039
                 (debye): [0.0  0.0  -0.000001]  Total: 0.000001

Nous pouvons comparer les résultats du VQE au solveur exact de NumPy et voir qu’ils correspondent.

calc = GroundStateEigensolver(transformation, numpy_solver)
res = calc.solve(driver)
print(res)

=== GROUND STATE ENERGY ===

* Electronic ground state energy (Hartree): -1.857275030202
  - computed part:      -1.857275030202
  - frozen energy part: 0.0
  - particle hole part: 0.0
~ Nuclear repulsion energy (Hartree): 0.719968994449
> Total ground state energy (Hartree): -1.137306035753

=== MEASURED OBSERVABLES ===

  0:  # Particles: 2.000 S: 0.000 S^2: 0.000 M: 0.000

=== DIPOLE MOMENTS ===

~ Nuclear dipole moment (a.u.): [0.0  0.0  1.3889487]

  0:
  * Electronic dipole moment (a.u.): [0.0  0.0  1.3889487]
    - computed part:      [0.0  0.0  1.3889487]
    - frozen energy part: [0.0  0.0  0.0]
    - particle hole part: [0.0  0.0  0.0]
  > Dipole moment (a.u.): [0.0  0.0  0.0]  Total: 0.
                 (debye): [0.0  0.0  0.0]  Total: 0.

Utiliser une fonction de filtre

Parfois, le véritable état au sol des Hamiltoniens n’est pas intéressant parce qu’il se trouve dans un autre secteur de symétrie de l’espace Hilbert. Dans ce cas, le NumPy eigensolver peut prendre une fonction de filtre pour retourner seulement les eigenstates avec par exemple le nombre correct de particules. Ceci est particulièrements important dans le cas des calculs de structures vibroniques où le véritable état au sol du Hamiltonien est l’état du vide. Une fonction de filtre par défaut pour vérifier le nombre de particules est implémentée dans les différentes transformations et peut être utilisée comme

from qiskit.chemistry.drivers import GaussianForcesDriver
from qiskit.chemistry.algorithms.ground_state_solvers import NumPyMinimumEigensolverFactory
from qiskit.chemistry.transformations import (BosonicTransformation,
                                              BosonicTransformationType,
                                              BosonicQubitMappingType)

driver = GaussianForcesDriver(logfile='aux_files/CO2_freq_B3LYP_ccpVDZ.log')
bosonic_transformation = BosonicTransformation(qubit_mapping=BosonicQubitMappingType.DIRECT,
                                               transformation_type=BosonicTransformationType.HARMONIC,
                                               basis_size=2,
                                               truncation=2)

solver_without_filter = NumPyMinimumEigensolverFactory(use_default_filter_criterion=False)
solver_with_filter = NumPyMinimumEigensolverFactory(use_default_filter_criterion=True)

gsc_wo = GroundStateEigensolver(bosonic_transformation, solver_without_filter)
result_wo = gsc_wo.solve(driver)

gsc_w = GroundStateEigensolver(bosonic_transformation, solver_with_filter)
result_w = gsc_w.solve(driver)

print(result_wo)
print('\n\n')
print(result_w)

=== GROUND STATE ENERGY ===

* Vibronic ground state energy (cm^-1): (1e-12+0j)
The number of occupied modals is
- Mode 0: [0.0, 0.0, 0.0, 0.0]



=== GROUND STATE ENERGY ===

* Vibronic ground state energy (cm^-1): (2536.487976362422+0j)
The number of occupied modals is
- Mode 0: [1.0000000000000002, 1.0000000000000002, 1.0000000000000002, 1.0000000000000002]

/Users/aul/anaconda3/envs/QiskitPip/lib/python3.6/site-packages/qiskit/chemistry/results/vibronic_structure_result.py:73: DeprecationWarning: The Python built-in `round` is deprecated for complex scalars, and will raise a `TypeError` in a future release. Use `np.round` or `scalar.round` instead.
  format(round(self.computed_vibronic_energies[0], 12)))
/Users/aul/anaconda3/envs/QiskitPip/lib/python3.6/site-packages/qiskit/chemistry/results/vibronic_structure_result.py:73: DeprecationWarning: The Python built-in `round` is deprecated for complex scalars, and will raise a `TypeError` in a future release. Use `np.round` or `scalar.round` instead.
  format(round(self.computed_vibronic_energies[0], 12)))

import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
Qiskit	0.23.0
Terra	0.16.0
Aer	0.7.0
Ignis	0.5.0
Aqua	0.8.0
IBM Q Provider	0.11.0
System information
Python	3.6.9 |Anaconda, Inc.| (default, Jul 30 2019, 13:42:17) [GCC 4.2.1 Compatible Clang 4.0.1 (tags/RELEASE_401/final)]
OS	Darwin
CPUs	2
Memory (Gb)	16.0
Tue Oct 20 18:05:31 2020 CEST

This code is a part of Qiskit

© Copyright IBM 2017, 2020.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.