Computação quântica em poucas palavras¶

A computação quântica representa um novo paradigma em computação que utiliza os princípios fundamentais da mecânica quântica para realizar cálculos. Se você está lendo isso, então você sem dúvida já ouviu que a promessa da computação quântica reside na possibilidade de realizar de forma eficiente um punhado de tarefas como a fatoração de primos, simulação quântica e otimização; computações cujos tamanhos estão além das capacidades até mesmo dos maiores dos computadores clássicos.

O poder da computação quântica baseia-se em dois pilares da mecânica quântica, nomeadamente a superposição e o emaranhamento que destacam os aspectos ondulatórios e a partículares da computação quântica, respectivamente. O Qiskit é uma SDK para executar cálculos quânticos que utilizam esses princípios mecânico quânticos usando o idioma de circuitos quânticos. Composto de portas quânticas, instruções e lógica de controle clássica, circuitos quânticos permitem expressar algoritmos e aplicações complexas de forma abstrata e que pode ser executada em um computador quântico. Em sua essência, o Qiskit é um mecanismo de construção, otimização e execução de circuitos quânticos. Algoritmos adicionais e camadas de aplicações alavancam circuitos quânticos, geralmente em conjunto com recursos de computação clássica, para resolver problemas de otimização, química quântica, física, aprendizado de máquina e finanças. No que segue, apresentamos uma breve visão geral da computação quântica e como o Qiskit é usado em cada passo. Os leitores interessados são direcionados para materiais detalhados adicionais para novas idéias.

Superposição¶

Tal como um computador clássico, um computador quântico opera em bits. No entanto, enquanto bits clássicos só podem ser encontrados nos estados 0 e 1, uma bit quântico, ou qubit, pode representar os valores 0 e 1, ou combinações lineares de ambos. Estas combinações lineares são conhecidas como superposições (ou estados de superposição) e permitem representar, e processar, um número exponencial de estados lógicos simultaneamente.

Para ver como esse recurso é utilizado na computação quântica começamos por recorrer a uma analogia clássica: o cancelamento de ruído. Cancelamento de ruído, como é feito no fones de ouvido com cancelamento de ruído, por exemplo, é executado utilizando o princípio da superposição juntamente com interferências para reduzir a amplitude do ruído indesejado gerando um tom com aproximadamente a mesma frequência e amplitude, mas fora de fase por um valor de \(\pi\) (ou qualquer outro multiplo inteiro ímpar de \(\pi\)).

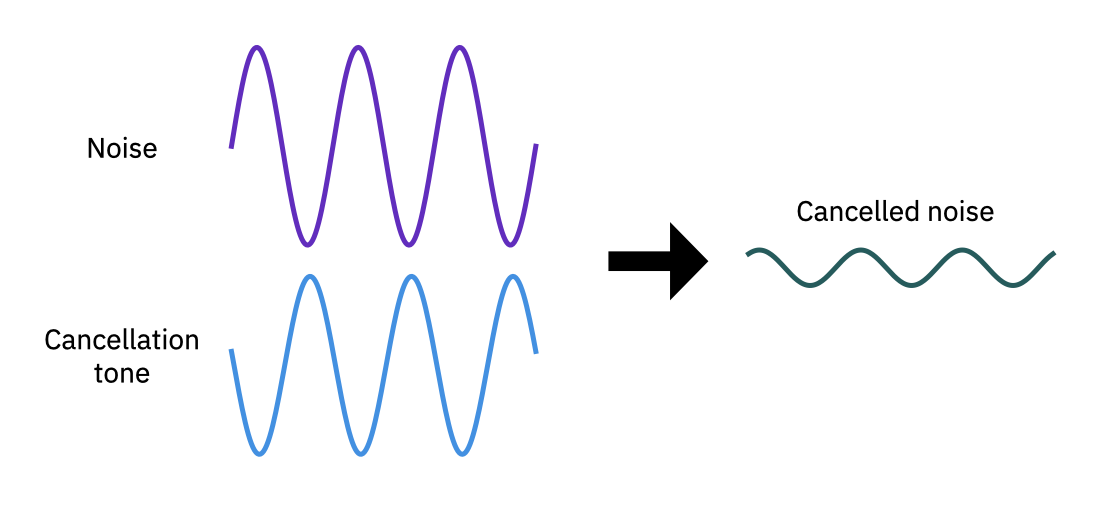
_images/noise_cancel.png — Fig. 1 Cancelamento aproximado de um sinal de ruído por um tom de amplitude quase igual e deslocamento por uma fase de \(\sim \pi\).¶

Como mostrado acima, quando a diferença de fase é próxima de um múltiplo ímpar de \(\pi\), a superposição das duas ondas resulta em interferência e um resultado que é significativamente reduzido comparado ao original. O resultado é o sinal de interesse livre de ruído. Embora este processamento seja feito por circuitos digitais, a amplitude e a fase são variáveis contínuas que nunca podem ser combinadas perfeitamente, resultando numa correção incompleta.

Uma computação geral em um computador quântico procede da mesma forma que o cancelamento de ruído. Para começar, se prepara uma superposição de todos os possíveis estados de computação. Isso é então usado como uma entrada para um circuito quântico que interfere seletivamente os componentes da superposição de acordo com um algoritmo prescrito. O que resta após o cancelamento das amplitudes e fases relativas do estado de entrada é a solução para o cálculo executado pelo circuito quântico.

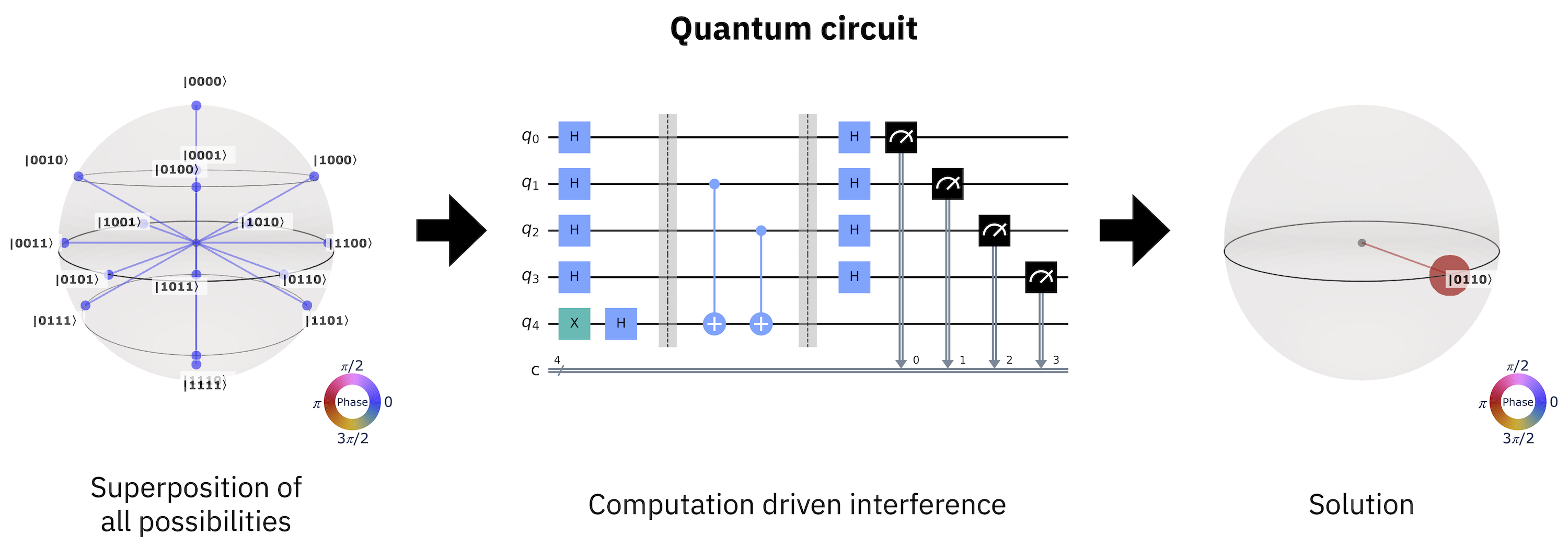
_images/quantum_interference.png — Fig. 2 Computação quântica como um processo de geração de interferência.¶

Entrelaçamento¶

O segundo princípio da mecânica quântica que a computação quântica pode utilizar é o fenômeno do emaranhamento. O emaranhamento se refere aos estados de mais de um qubit (ou partículas em geral) em que o estado combinado dos qubits contém mais informação do que os qubits independentemente. A esmagadora maioria dos estados quânticos de múltiplos qubits está emaranhada e representa um recurso valioso. Por exemplo, estados entrelaçados entre qubits podem ser usados para o teletransporte quântico, onde um estado emaranhado compartilhado de dois qubits pode ser manipulado para transferir informação de um qubit para outro independentemente da proximidade física relativa dos qubits. Estados entrelaçados, como estados naturais de sistemas quânticos, também são importantes em disciplinas como a química quântica e a simulação quântica onde a(s) solução(ões) geralmente tomam a forma de estados emaranhados multi-qubit. Também se pode utilizar estados quânticos altamente emaranhados de vários qubits para, por exemplo, gerar números aleatórios certificáveis. Há até mesmo um pacote Qiskit para fazer isso!

Circuitos Quânticos¶

Algoritmos e aplicações que utilizam recursos mecânico quânticos podem facilmente e eficientemente ser escritos na linguagem dos circuitos quânticos. Um circuito quântico é uma rotina computacional que consiste de operações quânticas coerentes em dados quânticos, tais como os mantidos em qubits, e simultaneamente computações clássicas em tempo real. Cada linha horizontal, ou o fio em um circuito representa um qubit, sendo a extremidade esquerda do fio os dados quânticos iniciais e o direito os dados quânticos finais gerados pela computação do circuito quântico. As operações nos qubits podem ser colocadas nesses fios e são representadas por caixas.

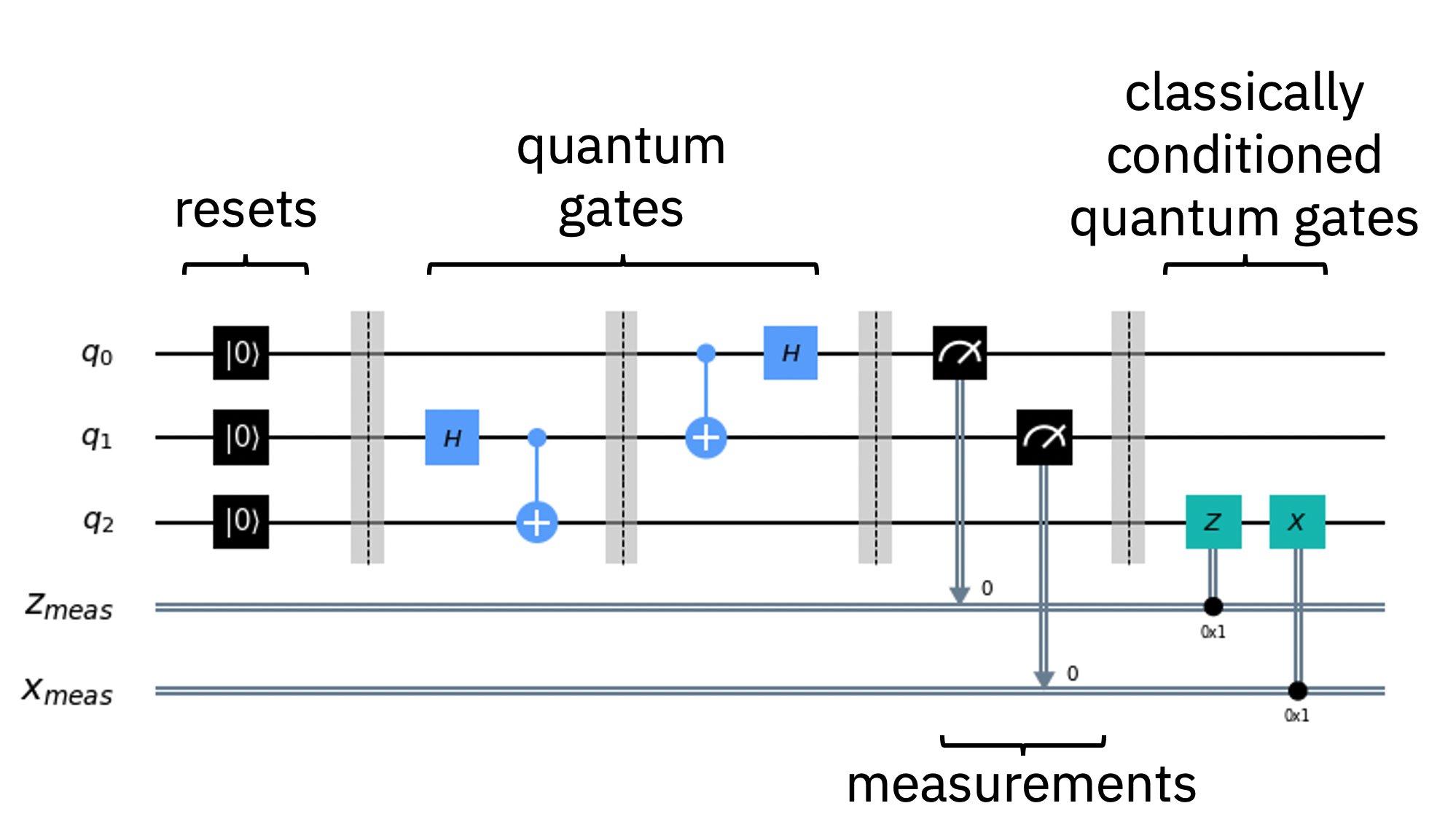
_images/teleportation_detailed.png — Fig. 3 Circuito de teletransporte quântico revisitado.¶

Os circuitos quânticos permitem que um computador quântico receba informação clássica e resulte em uma solução clássica. usando princípios quânticos como o da superposição e do emaranhamento para realizar a computação.

Um fluxo de trabalho de um algoritmo quântico típico consiste em:

O problema que queremos resolver,
Um algoritmo clássico que gera uma descrição de um circuito quântico,
O circuito quântico que precisa ser executado em hardware quântico,
E a solução clássica da saída para o problema que ele produz.

As portas quânticas formam as operações primitivas sobre dados quânticos. As portas quânticas representam transformações reversíveis e que preservam informação sobre os dados quânticos armazenados em qubits. Estas transformações “unitárias” representam o núcleo mecânico quântico de um circuito quântico. Algumas portas, como a \(X\) (também escrito como \(\oplus\)) e a \(CX\) têm analogos clássicos como operações de inversão de bit e \(XOR\), respectivamente, enquanto outros não têm. A porta de Hadamard (\(H\)) juntamente com as rotações parametrizadas \(rX(\theta)\) e \(rY(\theta)\), geram estados de superposição não clássicos enquanto portas como a \(Z\), \(rZ(\theta)\), \(S\), e \(T\) geram fases que podem ser usadas para interferência. Portas de dois qubit, como a \(CX\) são usadas para gerar emaranhamento entre pares de qubits, ou para “repassar” a fase de um qubit em outro. Em contraste com as portas, operações como a “medição”, representada pelo símbolo do medidor em uma caixa com uma linha se conectando a um fio “alvo”, extrai informações suficientes sobre o estado de um qubit, incluindo a fase, para ser capaz de representá-lo como um bit clássico e escrever o bit clássico no fio alvo (muitas vezes um fio totalmente clássico em algum dispositivo de leitura). Esta é a maneira típica de tirar informação dos dados quânticos para um dispositivo clássico. Note que com apenas \(H\), \(rZ(\theta)\), \(CX\) e portas de medição, isto é, um conjunto universal de portas, podemos construir qualquer circuito quântico, incluindo aqueles que computam eficientemente a dinâmica de qualquer sistema físico na natureza.

Algumas cargas de trabalho contêm uma sequência extensa de circuitos quânticos e computações clássicas intercalados, por exemplo, algoritmos variacionais quânticos executam circuitos quânticos dentro de um loop de otimização. Para estas cargas de trabalho, o desempenho do sistema aumenta substancialmente se os circuitos quânticos forem parametrizados, e as transições entre a execução do circuito e a computação clássica não simultânea forem eficientes. Consequentemente, nós definimos computação quase em tempo para se referir a computação com algoritmos que fazem uso repetido de circuitos quânticos com hardware desenvolvido para acelerar o tempo de computação. Na computação quase em tempo, a computação clássica ocorre em uma escala de tempo maior que a coerência da computação quântica. Contraste isso com computação em tempo real, onde o cálculo clássico ocorre dentro do tempo de decoerência do dispositivo quântico.

Construindo circuitos quânticos complexos com esforço mínimo está no coração do Qiskit. Com apenas algumas linhas de código, é possível construir circuitos complexos como o mostrado acima

qr = QuantumRegister(3, 'q')
cr = ClassicalRegister(2, 'zx_meas')
qc = QuantumCircuit(qr,cr)
qc.reset(range(3))
qc.barrier()
qc.h(1)
qc.cx([1,0],[2,1])
qc.h(0)
qc.barrier()
qc.measure([0,1], [0,1])
qc.barrier()
qc.z(2).c_if(cr, 1)
qc.x(2).c_if(cr, 2)

que suportam um rico conjunto de recursos de operações, e podem ser passadas para uma gama de computadores quânticos ou simuladores clássicos.

Computadores quânticos¶

_images/system_one.jpeg — Fig. 4 Uma vista dentro do IBM Quantum System One.¶

Computadores quânticos que são programados usando circuitos quânticos são chamados de computadores quânticos baseados em portas. Tais sistemas podem ser construídos a partir de qualquer tecnologia quântica que permita definir elementos de qubit e possa implementar operações de portas multi-qubit com alta fidelidade. Atualmente, arquiteturas baseadas em circuitos supercondutores, armadilhas de íons, pontos quânticos semicondutores, fótons e átomos neutros estão sendo desenvolvidos ativamente e muitos estão acessíveis aos usuários pela internet. O Qiskit é agnóstico em relação à arquitetura subjacente de um determinado sistema quântico, e pode compilar um circuito quântico para combinar com a topologia de porta emaranhada de um dispositivo quântico, mapear as instruções do circuito no conjunto de portas nativas do dispositivo e otimizar o circuito quântico resultante para uma fidelidade aprimorada.

Como no exemplo de cancelamento de ruído acima, a amplitude e a fase de qubits são graus de liberdade contínuos sobre os quais as operações nunca poderão ser feitas exatamente. Estes erros das portas, juntamente com o ruído do ambiente no qual um computador quântico reside, podem conspirar para arruinar um cálculo se não forem contabilizados no processo de compilação, e podem exigir procedimentos adicionais de mitigação a fim de obter um resultado de alta fidelidade nos sistemas quânticos atuais suscetíveis a ruído. O Qiskit é capaz de levar em conta uma ampla gama de métricas de calibração de dispositivos (veja a figura abaixo) na sua estratégia de compilação e pode selecionar um conjunto ideal de qubits para executar um determinado circuito quântico. Além disso, o Qiskit hospeda uma coleção de técnicas de mitigação de ruído para extrair uma representação fiel do resultado de um circuito quântico.

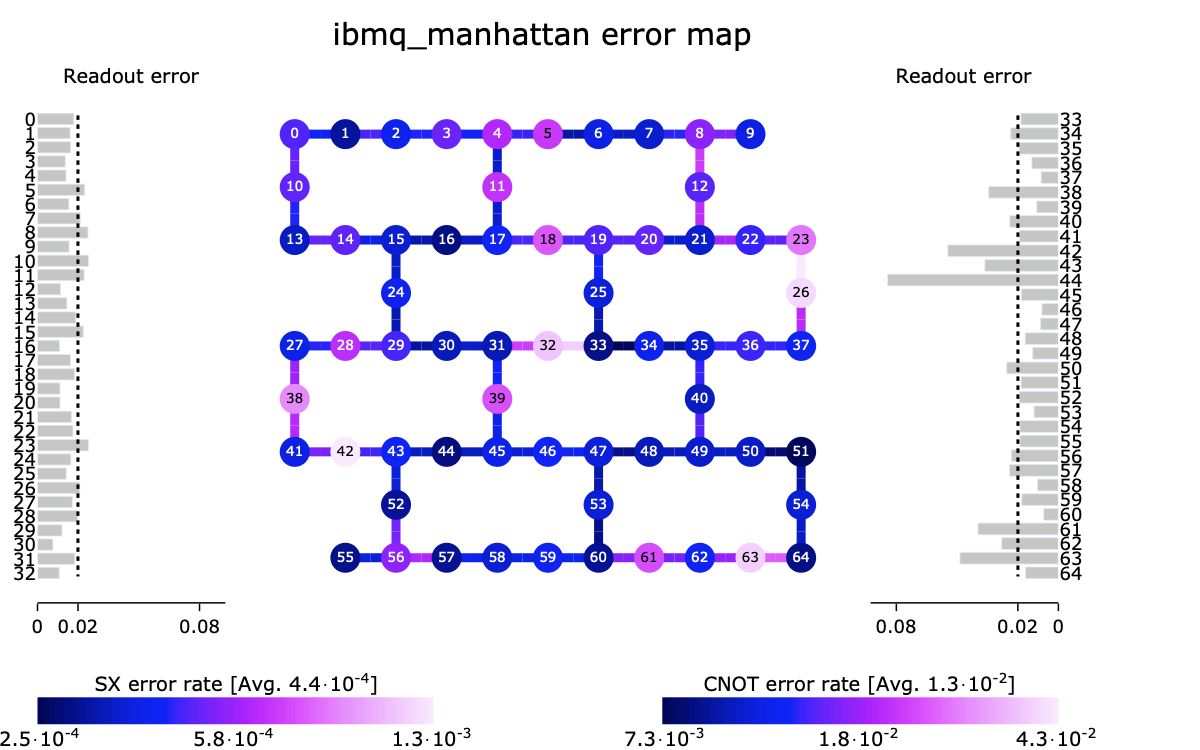
_images/system_error.png — Fig. 5 Topologia e taxas de erro para o sistema *ibmq_manhattan* do IBM Quantum.¶

Onde ir a partir daqui¶

Espero que tenhamos dado ao leitor um sabor do que a Computação Quântica tem para oferecer e que você esteja com fome de mais. Em caso afirmativo, há vários recursos que podem ser interessantes:

Getting started with Qiskit - Mergulhe diretamente no Qiskit.
Field guide to quantum computing : Uma introdução leve baseada em física escrita por alguns dos fundadores da computação quântica que faz uso do compositor de circuitos interativo.
Qiskit textbook : Um complemento de cursos universitários de algoritmos quânticos e computação quântica baseado no Qiskit.